Definition of Arithmetic Circuit
Let \(C: \ \mathbb{F}^n \ \rightarrow \ \mathbb{F}^k\) be a map which takes \(n\) arguments from a finite field \(\mathbb{F}\) as inputs and compute \(k\) outputs in \(\mathbb{F}\). \(C\) is an arithmetic circuit if the outputs are determined by the operations \(+\) and \(\times\) to the inputs. We assign the wires in the circuit as \(a_i \) where \(\ i \in {0,…,m}, a_0=1\). We may designate some of the input/output wires as a statement and use the left wires as a witness. A relation \(R\) is a statement that describes some witness wires satisfy the arithmetic circuit.
Given an example:
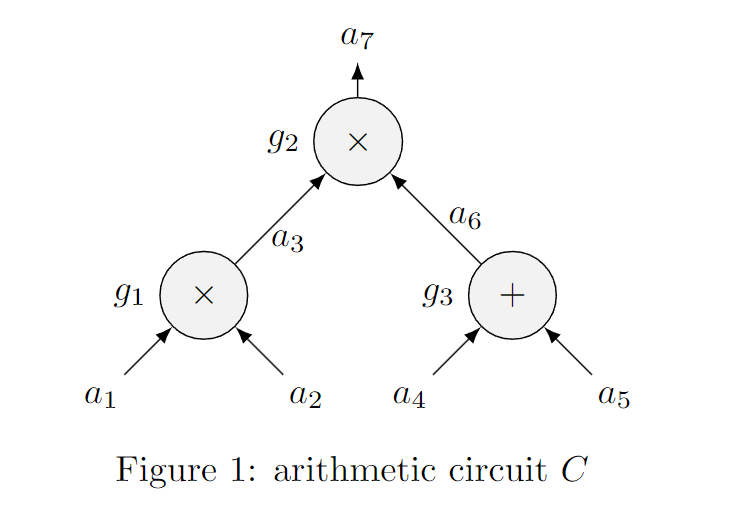
Transfer Arithmetic Circuit to Polynomials
The goal of Quadratic Arithmetic Programs in zk-SANRK is to transform the circuit to polynomials. Then the fact that a prover knows the coefficients of these polynomials is equivalent to that this prover knows valid assignments \((a_1,a_2,…,a_m)\in \mathbb{F}\) to the circuit.
QAP: Quadratic Arithmetic Programs
For a given circuit \(C\) with assignments \((a_1,a_2,…,a_m)\in \mathbb{F}\), a Quadratic Arithmetic Program \(Q(C)=(\{u_i(x)\}_{i=0}^m,\ \{v_i(x)\}_{i=0}^m,\ \{w_i(x)\}_{i=0}^m,t(x))\) is a set of polynomials satisfy the following equation:
$$\sum\limits_{i=0}^m a_i u_i(x) \cdot \sum\limits_{i=0}^m a_i v_i(x)=\sum\limits_{i=0}^m a_i w_i(x) + h(x)\cdot t(x)$$
The polynomial \(t(x)\) is called target polynomial.
Construction of QAP
In this section we describe how to construct an Quadratic Arithmetic Program for a circuit.
1. Write down all the constraint equation of the gates in the circuit in the format of:
(Left input) operator (right input) = output
For example:
\(a_i \times a_j=a_k\) for multiplication gate
\(1 \times (a_j+a_i)=a_k\) for addition gate
For circuit that has \(n\) gates, we will have \(n\) such equations.
From these equations, we construct:

\(u_{i,j}\) is the coefficient of \(a_i\) in the left input of the \(j\)-th constraint equation. \(v_{i,j}\) is the coefficient of \(a_i\) in the right input of the \(j\)-th constraint equation. \(w_{i,j}\) is the coefficient of \(a_i\) in the output of \(j\)-th constraint equation. \(\circ\) is an element-wise product operation.
For example:
A circuit has two constraints equation from two gates, they are:
\(a_1 \cdot a_2 = a_3\)
\(1 + (a_1+a_2)=a_4\)
Then we can have:

2. For every input \(a_i\), we use its coefficients \(\{u_{i,j}\}_{j=1}^n\) in different constraint to construct a polynomial \(u_i(x)\) with degree at most \(n-1\). Randomly choose \(r_1,…r_n\), let the construction of \(u_i(x)\) satisfies \(u_i(r_j)=u_{i,j}\). Use the same way to construct \(v_i(x),w_i(x)\).
After this step, we transfer the previous matrix equation in step 1 to a equation as following:
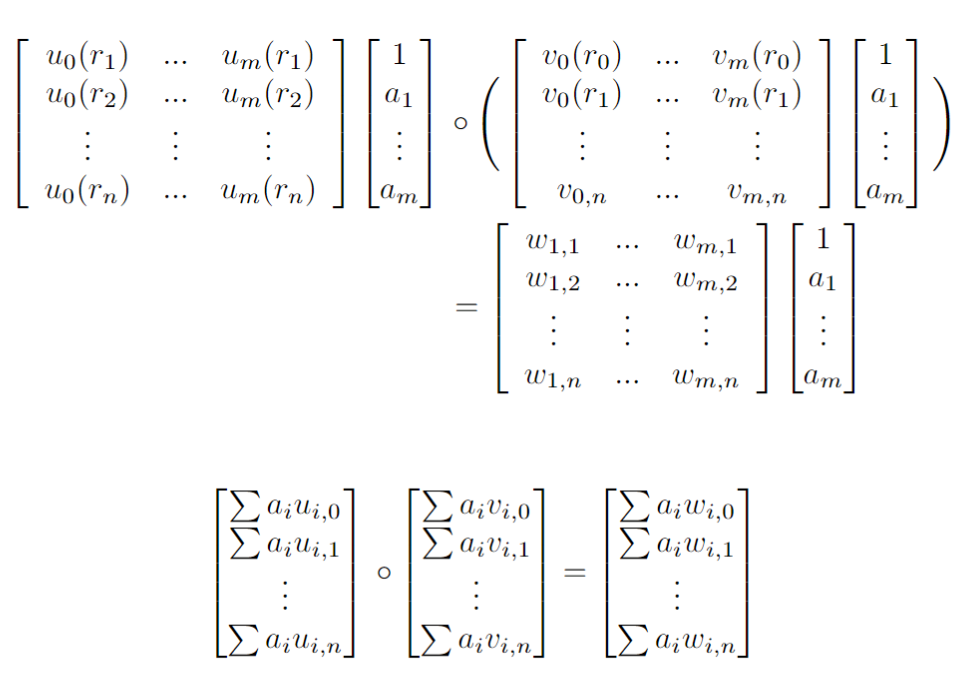
3. we get three set of polynomials:
\(\{u_i(x)\}_{i=0}^m\),\(\{v_i(x)\}_{i=0}^m\), \(\{w_i(x)\}_{i=0}^m\)
The following equation holds when \(x \in \{r_1,r_2,…,r_n\}\)
$$\sum\limits_{i=0}^m a_i u_i(x) \cdot \sum\limits_{i=0}^m a_i v_i(x)=\sum\limits_{i=0}^m a_i w_i(x) $$
Let
$$P(x)=\sum\limits_{i=0}^m a_i u_i(x) \cdot \sum\limits_{i=0}^m a_i v_i(x)-\sum\limits_{i=0}^m a_i w_i(x) $$
\(P(x)\) has roots \(r_1,r_2,…,r_n\).
Thus
$$P(x)=\sum\limits_{i=0}^m a_i u_i(x) \cdot \sum\limits_{i=0}^m a_i v_i(x)-\sum\limits_{i=0}^m a_i w_i(x)=h(x)t(x) $$
Then we get:
$$\sum\limits_{i=0}^m a_i u_i(x) \cdot \sum\limits_{i=0}^m a_i v_i(x)=\sum\limits_{i=0}^m a_i w_i(x) + h(x)\cdot t(x)$$
The equation above is called a quadratic arithmetic program for a circuit.
After almost 2 years working in the industry, I start miss the cryptographic challenges again, so I will start picking up my old notes that were written during my PhD, refine them and hope they can bring my old challenges back.