R1CS definitions

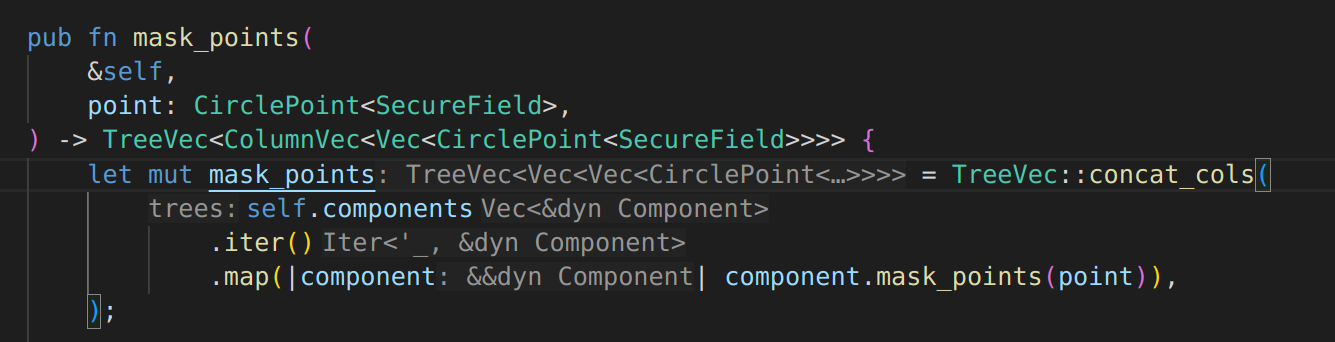
R1CS encoding
R1CS instance \(x=(\mathbb{F},A,B,C,io,m,n)\)
let \(Z=(io,1,w)\), then we have for example
\(\underbrace{\begin{bmatrix}0&1&1&0\\0&0&1&0\\…&…&…&..\\…&…&…&..\end{bmatrix}}_{A}\begin{pmatrix}w_1\\1\\w_2\\w_3\end{pmatrix}\circ \underbrace{\begin{bmatrix}0&1&0&0\\0&0&1&0\\…&…&…&..\\…&…&…&..\end{bmatrix}}_{B}\begin{pmatrix}w_1\\1\\w_2\\w_3\end{pmatrix}\)
\(=\underbrace{\begin{bmatrix}1&0&0&0\\0&0&0&1\\…&…&…&..\\…&…&…&..\end{bmatrix}}_{C}\begin{pmatrix}w_1\\1\\w_2\\w_3\end{pmatrix}\)
This express the constraints:
$$(1+w_2) \cdot 1=w_1$$
$$w_2 \cdot w_2=w_3$$
(here \(w_1\) is public input/output )
In order to use the sum-check protocol, we need to encode R1CS in a different way, as sum-check is about binary representations, therefore, it ends up something like this:
\(s=[\log m]\)
\(F_{io}(x)=\left(\sum\limits_{y\in\{0,1\}^s}A(x,y)\cdot Z(y)\right)\cdot \left(\sum\limits_{y\in\{0,1\}^s}B(x,y)\cdot Z(y)\right)\)
$$-\left(\sum\limits_{y\in\{0,1\}^s}C(x,y)\cdot Z(y)\right)$$
view \(x\) as the row number and \(y\) as the column, let me write the above equation in another way:
\(\underbrace{\begin{bmatrix}\widetilde{A}([00],[00])&\widetilde{A}([00],[01])&\widetilde{A}([00],[10])&\widetilde{A}([00],[11])\\\widetilde{A}([01],[00])&\widetilde{A}([01],[01])&\widetilde{A}([01],[10])&\widetilde{A}([01],[11])\\…&…&…&..\\…&…&…&..\end{bmatrix}}_{A}\begin{pmatrix}z([00])\\z([01])\\z([10])\\z([11])\end{pmatrix}\)
\(\circ \underbrace{\begin{bmatrix}\widetilde{B}([00],[00])&\widetilde{B}([00],[01])&\widetilde{B}([00],[10])&\widetilde{B}([00],[11])\\\widetilde{B}([01],[00])&\widetilde{B}([01],[01])&\widetilde{B}([01],[10])&\widetilde{B}([01],[11])\\…&…&…&..\\…&…&…&..\end{bmatrix}}_{B}\begin{pmatrix}z([00])\\z([01])\\z([10])\\z([11])\end{pmatrix}\)
\(=\underbrace{\begin{bmatrix}\widetilde{B}([00],[00])&\widetilde{B}([00],[01])&\widetilde{B}([00],[10])&\widetilde{B}([00],[11])\\\widetilde{B}([01],[00])&\widetilde{B}([01],[01])&\widetilde{B}([01],[10])&\widetilde{B}([01],[11])\\…&…&…&..\\…&…&…&..\end{bmatrix}}_{C}\begin{pmatrix}z([00])\\z([01])\\z([10])\\z([11])\end{pmatrix}\)
\(=\begin{pmatrix}\left(\sum\limits_{y\in\{0,1\}^2}A([00],y)z(y)\right)\cdot\left(\sum\limits_{y\in\{0,1\}^2}B([00],y)z(y)\right)-\left(\sum\limits_{y\in\{0,1\}^2}C([00],y)z(y)\right) \\\left(\sum\limits_{y\in\{0,1\}^2}A([01],y)z(y)\right)\cdot\left(\sum\limits_{y\in\{0,1\}^2}B([01],y)z(y)\right)-\left(\sum\limits_{y\in\{0,1\}^2}C([01],y)z(y)\right)\\z([10])\\z([11])\end{pmatrix}\)
\(=\begin{pmatrix}\widetilde{F}_{io}([00])\\\widetilde{F}_{io}([01])\\\widetilde{F}_{io}([10])\\\widetilde{F}_{io}([11])\end{pmatrix}\)
til this point if we can prove \(\widetilde{F}_{io}(x)=0\), then the witness exist.
Now come to Lemma 4.1 in Spartan paper, the conclusion is straight forward.

Til now we only talk about sum-check protocol with variate \(y\in \{0,1\}^s\), we would like one more layer of sum-check, namely, make \(x\) also into variate.
let
\(\mathcal{Q}_{io}(t)=\sum\limits_{x\in \{0,1\}^s}\widetilde{F}_{io}(x)\cdot \widetilde{eq}(t,x)\)
where \(\widetilde{eq}(t,x)=\prod\limits_{i=1}^{s}(t_i\cdot x_i +(1-t_i)\cdot (1-x_i) )\), \(t_i\) is the bitwise representation of \(t\)
short explanation for the equation:
\(\widetilde{eq}(t,x)\) only equal to 1 when \(t=x\), \(x\in \{0,1\}^s\) only count the point on hypercube, note here each bit (totally s bits) in multilinear setting represent a variable.
it is more precise to present \(\mathcal{Q}_{io}(t)\) as \(\mathcal{Q}_{io}(t_0,t_1,…,t_s)\). it is a multilinear/multi variables polynomial! as you can see in the picture below \(\mathcal{Q}_{io}(\tau)=0 … \tau \in_R \mathbb{F}^s\)
from above equation, a conclusion is

then lemma 4.3 give a proof that we can use “checking a random point evaluation of \(\mathcal{Q}_{io}(\tau)\) is 0 or not” to convince \(F_{io}(\cdot)\) evaluated to 0 at all points on hypercube.
define:
\(\mathcal{G}_{io,\tau}(x)=\widetilde{F}_{io}(x)\cdot \widetilde{eq}(\tau,x)\)
where \(\widetilde{eq}(t,x)=\prod\limits_{i=1}^{s}(t_i\cdot x_i +(1-t_i)\cdot (1-x_i) )\), \(t_i\) is the bitwise representation of \(t\)
\(\mathcal{Q}_{io}(\tau)=\sum\limits_{x\in \{0,1\}^s}\mathcal{G}_{io,\tau}(x)=\sum\limits_{x\in \{0,1\}^s}\widetilde{F}_{io}(x)\cdot \widetilde{eq}(\tau,x)\)
Our goal is to check if \(\mathcal{Q}_{io}(\tau)=0\) in this step,
=> it also means, checking \(\sum\limits_{x\in \{0,1\}^s}\mathcal{G}_{io,\tau}(x)=\sum\limits_{x\in \{0,1\}^s}\widetilde{F}_{io}(x)\cdot \widetilde{eq}(\tau,x)\) is 0
=> if and only if \(\widetilde{F}_{io}(x)=0\)
this now the theorem 4.3 is proved:
Let’s move to post 3.