Start with the proof of stwo:

commitmentSchemeProof
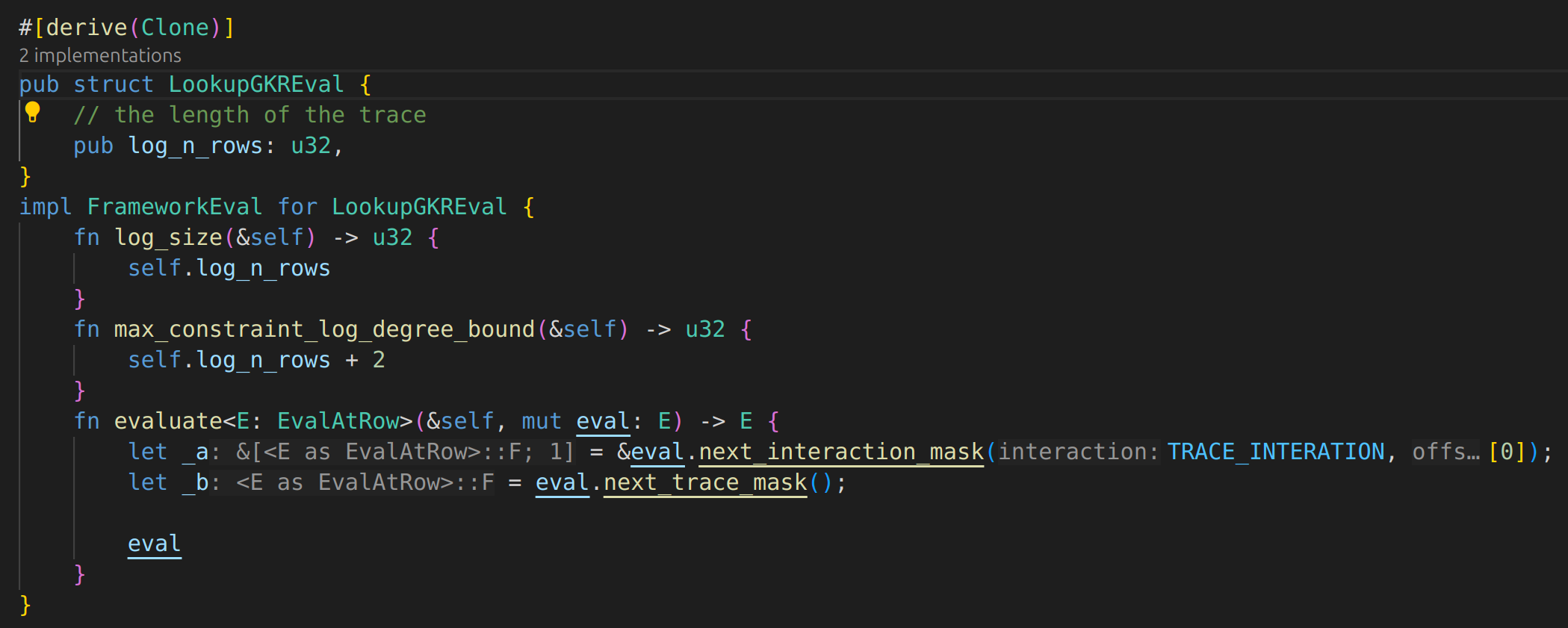
proof.commitments
contains the proof info, the interesting part is the commitments, in the verification function, there will be commitments[0], commitments[1],commitments[2] represent the commitment of pre-process trace, witness trace and lookup trace commitments. namely, they only have three root commitments, every root commitment should contains the info of many cols. need to figure out how.
the execution print info verify the proof.commitments indeed only has three elements:

output is

how these three root commits are built?
start with commitment to the column
- create a CommitmentSchemeProver
- commitment to the pre-processed columns

commitment_scheme.tree_builder function create a TreeBuilder that contains commitment_scheme itself as one of its elements.

polys of treebuilder contains all the polynomials
the extend_eval function first interpolate the trace to be poly, then extend the stored polys.

tree builder commit calls the commitmentProver commit functon, take all the polys of this as input

commitmentProver commit function create a new commitmentTreeProver, store in trees.
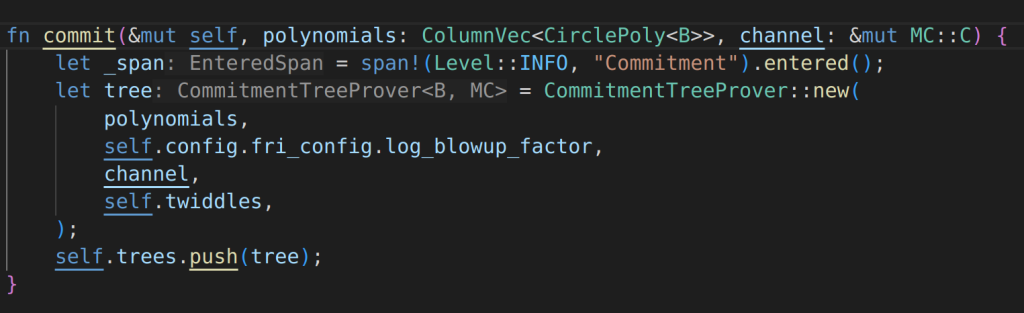
The CommitmentTreeProver is defined as

one tree builder is corresponding to many polynomials, but only one commitment.
- proof created in the prove function, checking the commitments are?
in the prove function, the proof is created here, we need to check the prove_values function, as it returns CommitmentSchemeProof, which has commitments

the prove_values is a function of commitmentProver, it creates commitmentSchemeProof like this, the interesting part is the commitments field, which take roots(), it create “roots” of tree root.
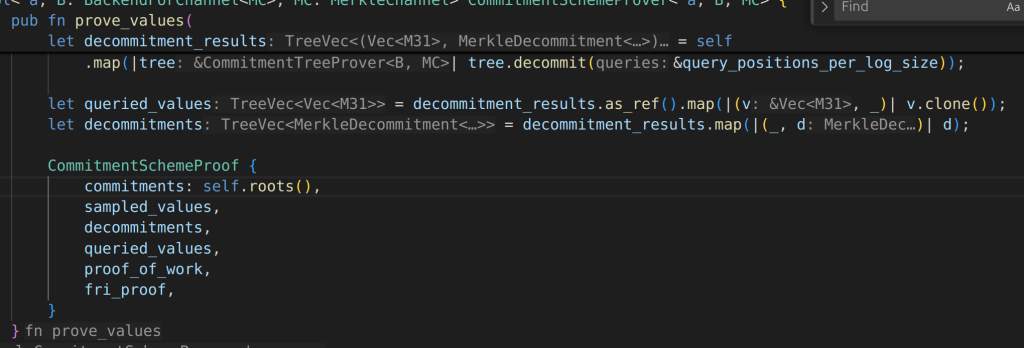
- CommitmentSchemeProver.roots()

it get root of every tree, now we just need to check of the root of a tree is buildt.
it just take the first layer of the merkle tree, which is the root.
each tree_build end up as a commitment root.
this commitment root comes from many columns, it from all the preprocess columns, or all the witness columns, or all the lookup colums.
so the next post, it to discover how this merkle tree is built to include many columns.