Committed Traces
The traces that will be interpreted as multilinear polynomial evaluations from STARK:
talking about a single lookup relation, for multiple lookup, it means the
Extra traces that dedicated for Logup-GKR and need to be built additionally
Circuit Example:
using a simple example to describe the GKR circuit
bus sends traces: \(a(w)\), \(b(w)\)
bus receive traces: \(c(w)\)
multiplicity: \(m(w)\)
GKR-circuit following MidenVM
length of these traces are all 4, concatenate them to get a trace with total length 16, then I need 4 bit to represent 16 values, meaning there will be a 4-variate polynomial to represent the input layer.
re-write the GKR-encoded traces as
bus sends traces: \(a(w)\), \(b(w)\)
bus receive traces: \(c(w)\)
multiplicity: \(m(w)\)
GKR-circuit General design
length of these traces are all 8, then I need 3 bits to represent 16 values, meaning there will be a 3-variate polynomial to represent the input layer.
re-write the GKR-encoded traces as
bus sends traces: \(a(w(i_0,i_1,i_2,i_3))\), \(b(w(i_0,i_1,i_2,i_3))\)
bus receive traces: \(c(w(i_0,i_1,i_2,i_3))\)
multiplicity: \(m(w(i_0,i_1,i_2,i_3))\)
Notes:
- in powdr, the receive table is not usually the same length with the sends, so it doesn’t make send to build the circuit like MidenVM: left input is send, right input is receive.
- I can concatenate all the send traces together to become a very wide input trace for GKR, but then it will have different length as the “machine trace”, if keeping the GKR input trace the same length as the machine trace, it make sense to use random linear combination to combine the end sum of each send trace, Miden does this similar way
- the important thing of above circuit is, I should only use one Lagrange basis column.
circuit:
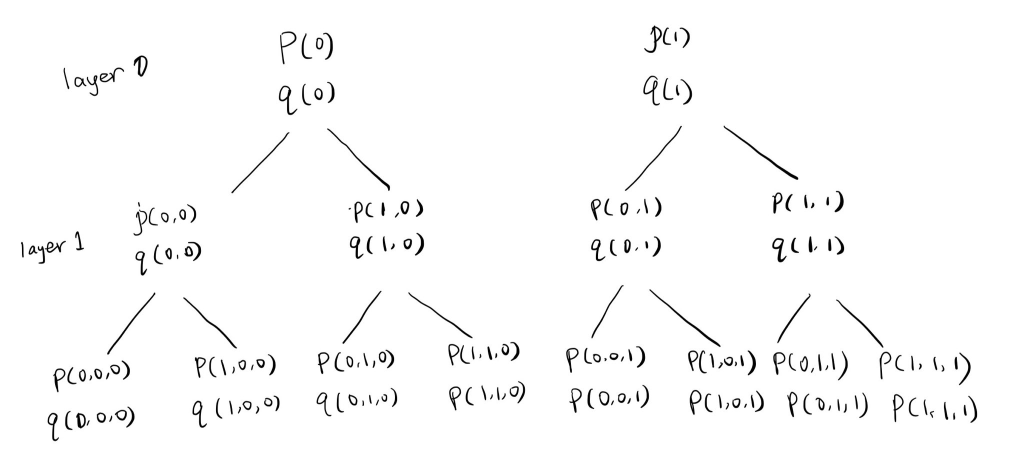
In the last layer, the prover ends up in proving the claims \(p(0,\rho_0,\rho_1),p(1,\rho_0,\rho_1),q(0,\rho_0,\rho_1),q(1,\rho_0,\rho_1)\), which further reduce to \(p(\rho_2,\rho_0,\rho_1),q(\rho_2,\rho_0,\rho_1)\)
\(p(\rho_2,\rho_0,\rho_1)\) are numerators, in most cases are 1s, apart from multiplicities.
\(q(\rho_2,\rho_0,\rho_1)=\widetilde{f_a}(\rho_2,\rho_0,\rho_1)+\alpha\)
Motivation for logup-GKR more clear, for Powdr implementation:
The constraint degree limitation in Miden doc description:
Following the description of this tutorial, the accumulator is built among several witness columns (think it as several bus sends), this is related to the parameter \(j\)

for each cell in accumulator, the element is computed among \(k\) columns at the same row, and also subtract the values in the table, i.e. \(b_{ij}\):

Then the degree limitation in each row is obvious: there are several fractions to be added in each row.
In powdr:
The constraint degree limitation occurs when batching accumulators: add the same row of different accumulators together to reduce committed accumulator column.