GKR circuit:
a layer in GKR : prover>src>core>lookups>gkr_prover.rs>layer
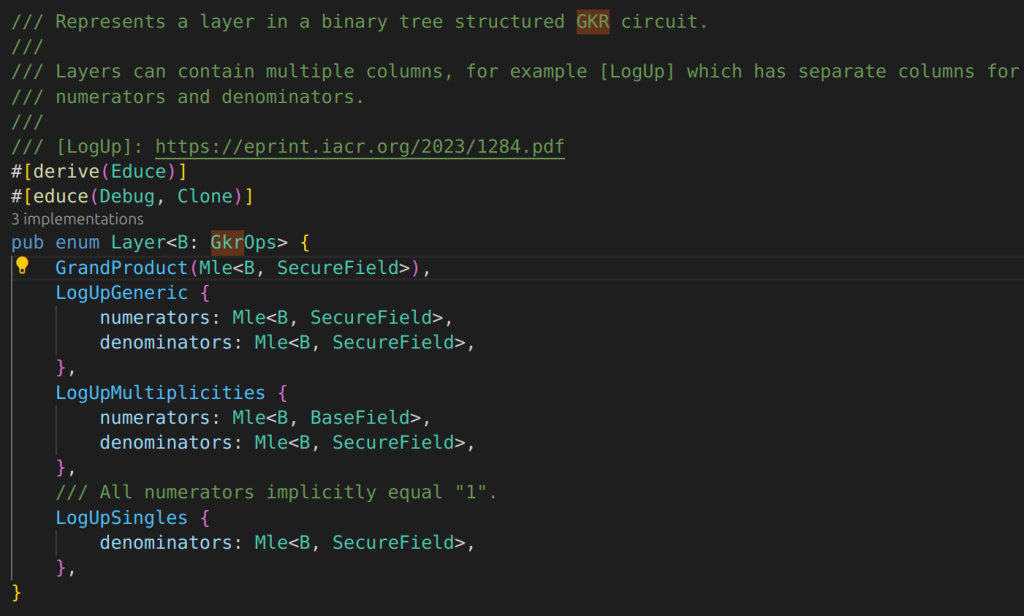
they take Mle: multi-linear extension as “input”.
Mle: core>lookups>mle.rs
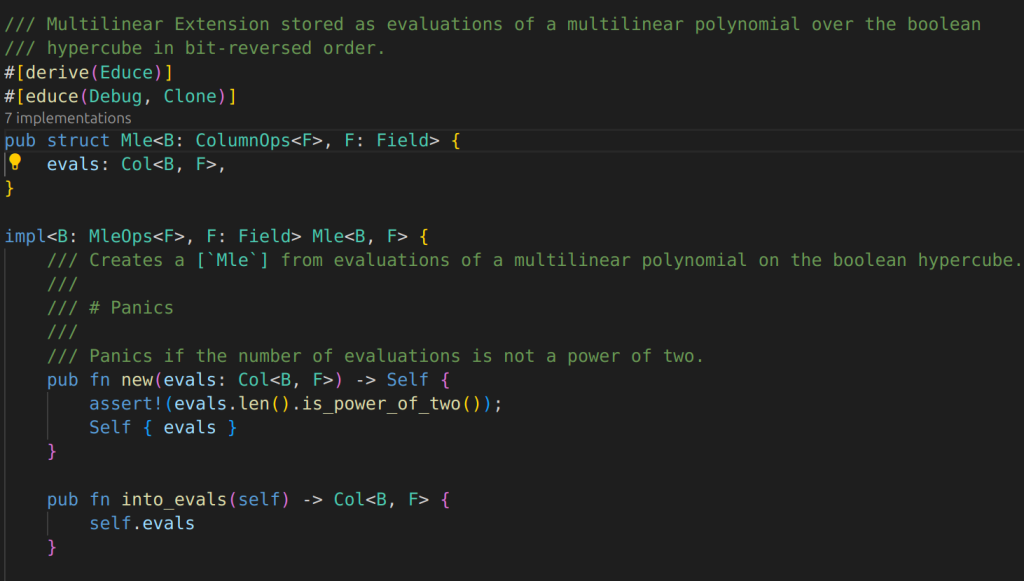
stored its evaluations on boolean hypercube, which is enough to uniquely determined the MLE
come back to the GKR layer struct, search where LogUpGeneric is used.
in backend>simd>lookups>gkr.rs there is several gkr test cases:
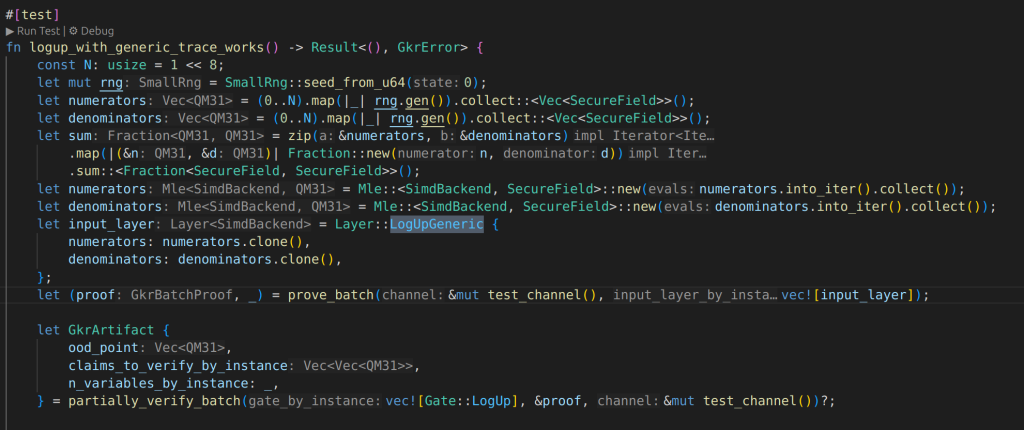
it also has prove function: prove_batch, the question is that this function seems to be purely computing fraction addition, how can it be embedded to the STARK proof systems.
need a different PIOP?
MLE evalution test example
checking this example to prove an evaluation for a multi-linear extension evaluation.
generates MLE using random values in secure field (combine with STARK, this would be the lookup table elements and the values send to the lookup table). all the coefficients are considered into a column.

two traces are committed, important to understand how they are built.

one trace is the coefficients of the multi-variate polynomial
one trace should include Lagrange basis and a running sum
one trace is the multi-variate Lagrange basis (the eq function), the other one is the running sum. in this example, the multi-linear polynomial comes from randomness, in STARK, they will come from a trace, so now I need to find out how to embedded a trace to create this multi-linear polynomial.
Lagrange kernel trace and running sum trace
these two traces come from this build_trace
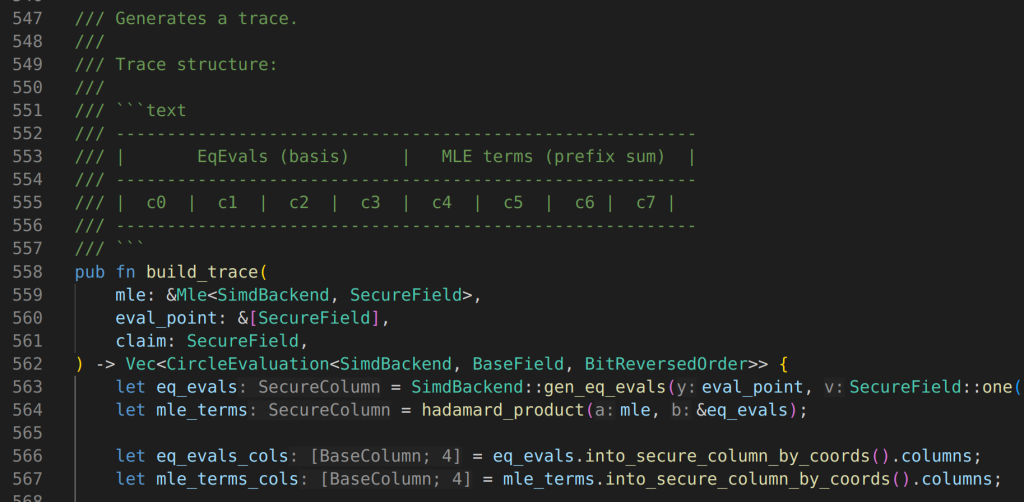
let’s first check eq_evals:
it should be something like:

\(x\) needs to be bit de-composite, it is the row number

eval_point should have the same number as de-composite x
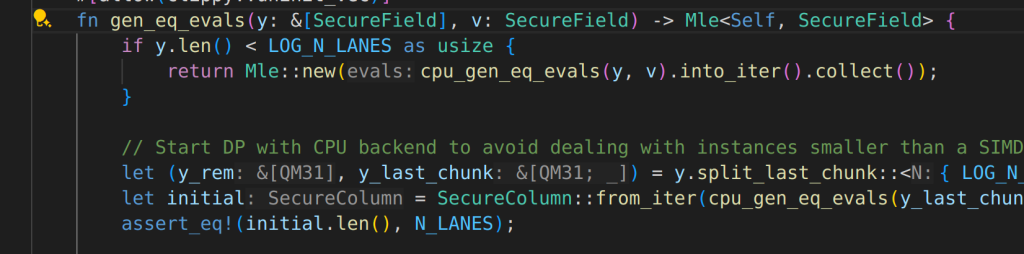
I will understand it from cpu implementation
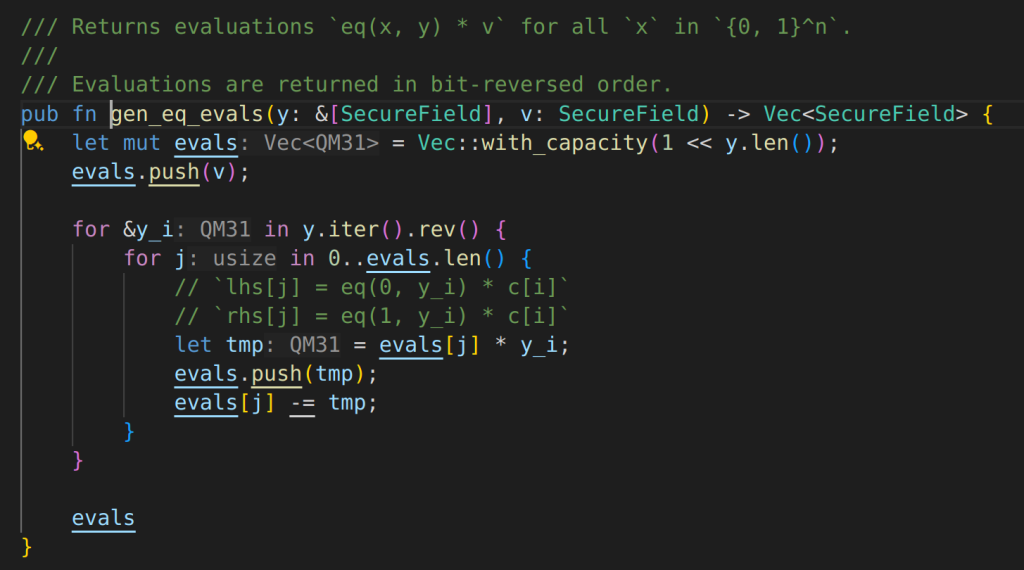
nice algorithm to compute Lagrange kernel
then its the running sum trace:

for a single trace example (\(m=1\)), this becomes:
\(\sum\limits_{x \in \{0,1\}^{\mu}}eq(x,\rho) f(x)\)
the trace looks like

the pre-fix is added purely to make a universal constraint. so til this point, let’s look at the constraint on these two columns first.
in the code, stwo computes the hadamard product first :

The constraint for the running sum column

let’s understand dome data structure here:
PackedM31: packed 16 elements into one

this code here is for the sum trace, prefix
