Follow my first post for Spartan
Closed-form expression for evaluating a polynomial
The closed-form expression for evaluating a polynomial \(\mathcal{G}(\cdot)\) at \((r_1,…,r_m)\in \mathbb{F}^m\) is
$$\mathcal{G}(r_1,…,r_m)=\sum\limits_{x\in\{0,1\}^m}\mathcal{G}(x)\prod\limits^{m}_{i=1}\underbrace{(r_i\cdot x_i + (1-r_i)(1-x_i))}_{x_i=0 \rightarrow 1-r_i, x=1 \rightarrow r_i }$$
emphasize:
\(r_i \in \mathbb{F}\)
\(x \in \{0,1\}^m\)
\(x_i \) is 0 or 1
Explain:
the key idea: the above polynomial has the same evaluations on hypercube (when \(r_i\in \{0,1\}\)) as \(g(x), x\in \{0,1\}^m\)
Given an example:
| \(r_1\) | \(r_2\) | \(g(\cdot,\cdot)\) |
| 0 | 0 | \(g(0,0)\) |
| 0 | 1 | \(g(0,1)\) |
| 1 | 0 | \(g(1,0)\) |
| 1 | 1 | \(g(1,1)\) |
The intuitive way to get LDE multilinear polynomial is directly write the polynomial according to the table:
\(g(r_1,r_2)=g(0,0)(1-r_1)(1-r_2)+ g(0,1)(1-r_1)r_2\)
\(+ g(1,0)r_1(1-r_2)+g(1,1)r_1r_2\)
namely, add term \(r_1\) when \(r_1=1\), add term \((1-r_1)\) when \(r_1=0\)
It is essentially the same as the closed form expression, which is general and beautiful.
Some facts:
- multilinear polynomial: \(\mathbb{F}^m \rightarrow \mathbb{F}\)
- Dense representation:\( DenseRepr(\mathcal{G}): \{0,1\}^m \rightarrow \mathbb{F}\)
relation between 1 and 2: multilinear polynomial can be represented uniquely by the list of evaluations over the Boolean hypercube
A very similar concept, which is used often in Binius, is multi-linear Lagrange basis, see the next section.
Multi-linear Lagrange basis
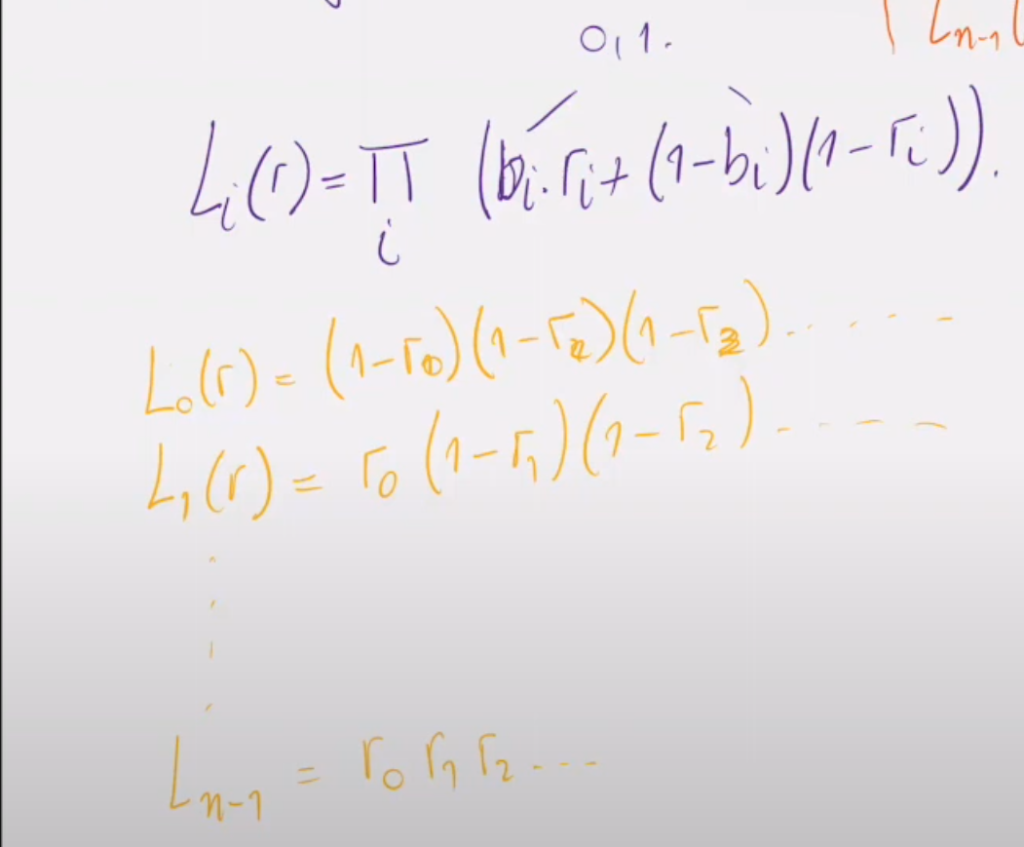
recall what is the problem we want to solve when we need Lagrange basis.
we know the evaluations of a polynomial at some points, we want to interpolate it back to its coefficient format.
in multilinear context, in binius or sumcheck, we often refer to the evaluations points are the points on the hypercube. so Lagrange basis in this setting, would be the basis that evaluate as 1 in one point of the hypercube, 0 on the other points on hypercube.
Lagrange basis:
$$\mathcal{L_i}(r_1,…,r_m)=\prod\limits^{m}_{i=1}\underbrace{(r_i\cdot b_i + (1-r_i)(1-b_i))}_{b_i=0 \rightarrow 1-r_i, b=1 \rightarrow r_i }$$
\((r_1,…,r_m)\) is the bitwise representation of \(r\)
Dense and Sparse representation for multilinear polynomials
A multilinear polynomial \(\mathcal{G}: \mathbb{F}^m \rightarrow \mathbb{F} \) is a sparse multilinear polynomial if \( |DenseRepr(\mathcal{G})| \) is sub-linear in \(O(2^m)\), otherwise, it is a dese multilinear polynomial
Polynomial commitment scheme for multi-linear polynomials
4 algorithms: setup, commit, open, Eval
\(b\leftarrow \mathbb{Eval}(pp,C,r,v,\mu; \mathcal{G,S})\)
\(\mathcal{P}\) attempts to convince \(\mathcal{V}\) that \(\mathcal{G}(r)=v\)