Plonk argument of knowledge can be described in 5 steps in a high level:
- Computation
- Arithmetic circuit
- Constrain System
- Transfer the constrain system to polynomial
- Prove gate constraints are satisfied.
- Prove permutation constraints are satisfied.
Constrain System in Plonk (Plonkish constrain system)
The constraint system in Plonk is
$$(\textbf{q}_{\textbf{L}_i} )\cdot x_{a_i}+(\textbf{q}_{\textbf{R}_i} )\cdot x_{b_i}+(\textbf{q}_{\textbf{O}_i} )\cdot x_{c_i}+(\textbf{q}_{\textbf{M}_i} )\cdot (x_{a_i}x_{b_i})+(\textbf{q}_{\textbf{C}_i} )=0$$
Transfer the constrain system to polynomial
There are 12 polynomial in total:
3 witness polynomials: \(a(X),b(X),c(X)\), represent the left, right inputs and the outputs of the gates.
5 selector polynomials: \(q_M(X), q_L(X),q_R(X),q_O(X),q_C(X)\), these polynomials are the public input and computed from the circuit
3 permutation mapping polynomials: \(S_{\sigma 1}(X),S_{\sigma 2}(X),S_{\sigma 3}(X)\) these polynomials are the public input and computed from the circuit
1 permutation polynomial: \(z(X)\)
$$z(w)=1$$
$$z(w^i)=\prod\limits_{j=2}^i\frac{(w_j^j+\beta w^j+\gamma)(w_{n+j}+\beta k_1 w^j+\gamma)(w_{2n+j}+\beta k_2 w^j+\gamma)}{ (w_j^j+\sigma^(j)\beta w^j+\gamma)(w_{n+j}+\sigma^(n+j)\beta k_1 w^j+\gamma)(w_{2n+j}+\sigma^*(2n+j)\beta k_3 w^j+\gamma)} $$
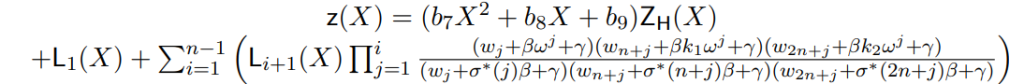
later will prove conditions:
this utilizes the lipton trick.
Prove gate constraints are satisfied.

Prove the permutation holds
