After understanding of the folding scheme of relaxed R1CS, of which the key idea is you can “fold” two proofs to be one, with this ability of relaxed R1CS in mind, how can one build a recursive proof from scratch? in this note I will describe several attempts to build a recursive proof, the aim is to help me understand Nova.
The content is mostly based on https://learnblockchain.cn/article/6429 (in Chinese)
IVC and ZKP
IVC aiming to provide one accumulated relaxed R1CS proof at the end for the recursive long-running computation.
The execution of long-running computation can be represented as

To generate proofs, the function \(F\) will be transformed to circuit, as most of the zkp system, output the result of the computation and a proof at the same time.
The first attempt
If we only have a zkp, how can we build a recursive proof system? The simple way is for each execution of the function, we generate a proof and do a verification (zkp is based on R1CS).
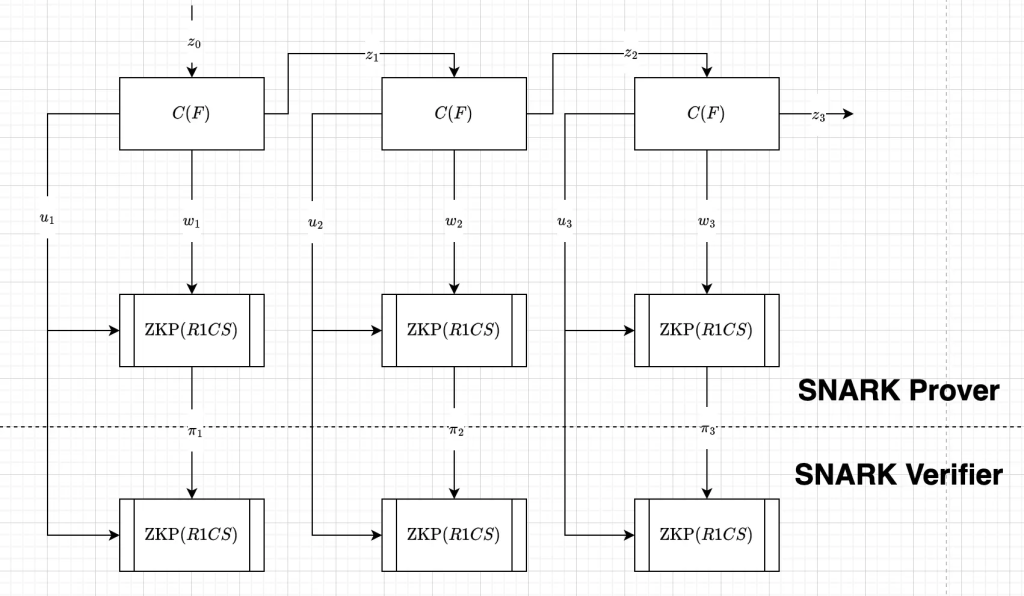
\(u_i\) here is the public input. But this is not recursive, to make it recursive, we can write the zkp verification into the function, so the execution of the function also verify the previous step is correct. However, this requires a sublinear verifier, otherwise, the circuit of each execution will become bigger and bigger. Precisely, in the first execution, the circuit size is \(|F|\), the second execution has size \(|F|+|V_1|\), the size of the third execution will become \(|F|+|V_1|+|V_2|\)…,as you can see, linear verifier is problematic. To solve this problem, IVC comes, it delay the linear verification computation til the end, and also fold each proof instance to become one proof.
The second attempt
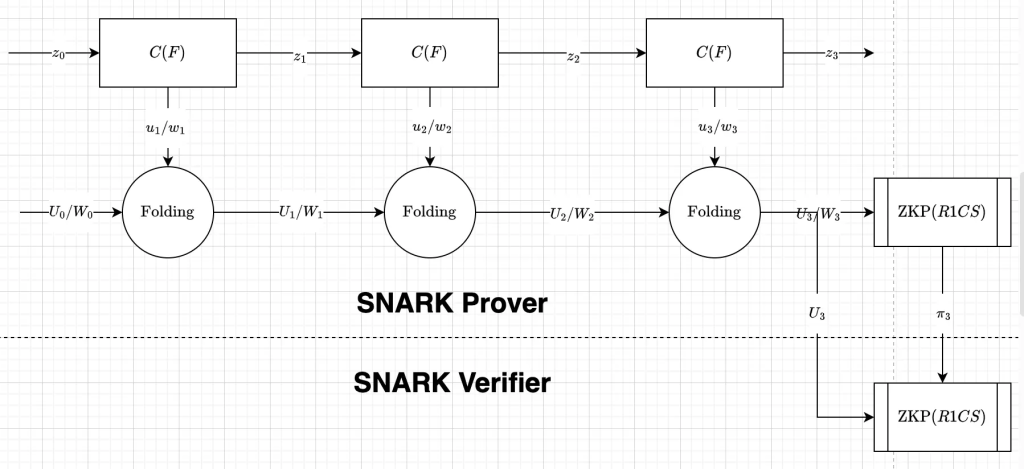
unfortunately here I will change the meaning of the notation \(u_i\), now it represents a commitment for R1CS (strictly satisfiable). Now at the beginning, we initialize an empty R1CS commiment instance, for every execution, a new R1CS commitment instance is generated and be folded to the running instance (accumulator). At the end the prover only give one relaxed R1CS commitment to the zkp prover. However, the folding process here is done by the prover, how can you prove the prover did the folding process correctly?
The third attempt
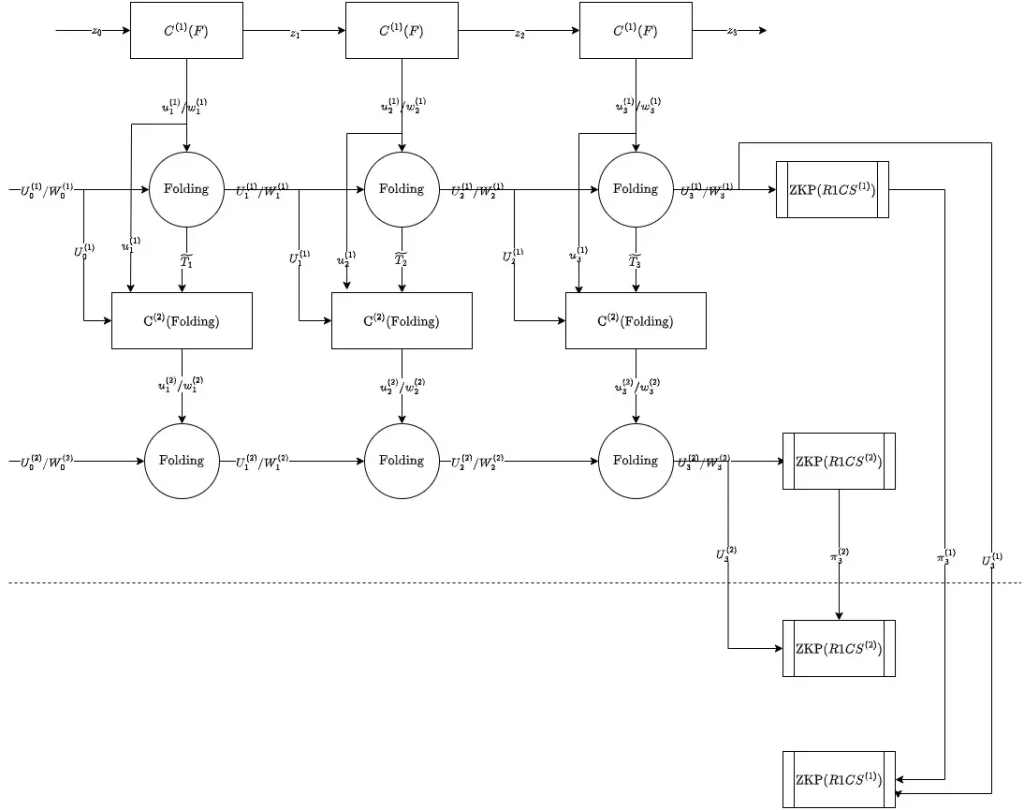
we can again generate a proof for the folding process, which means, write the folding process into a circuit. By doing this, we will get an extra proof for each execution of the real function \(F\), til now, let’s summarize what proofs we have for each execution of function \(F\).
- a proof for the execution of \(F\)—–accumulated to the accumulator
- an accumulator accumulate the proof of the execution proof of \(F\), itself is also a proof, relaxed R1CS commitment
- an proof of the folding process of accumulator.
the last proof will be generated for each execution of \(F\), so again, we need an accumulator to accumulate it. But you might notice, every time we introduce a proof for the folding process, we need to introduce an accumulator, which means we introduce another folding process, a proof for the folding process again … this doesn’t work, it went to an infinite loop.
The fourth attempt
To solve the infinite loop in the third attempt, we can write the prover of the folding process \(C^{(2)}\) into the function \(F\)
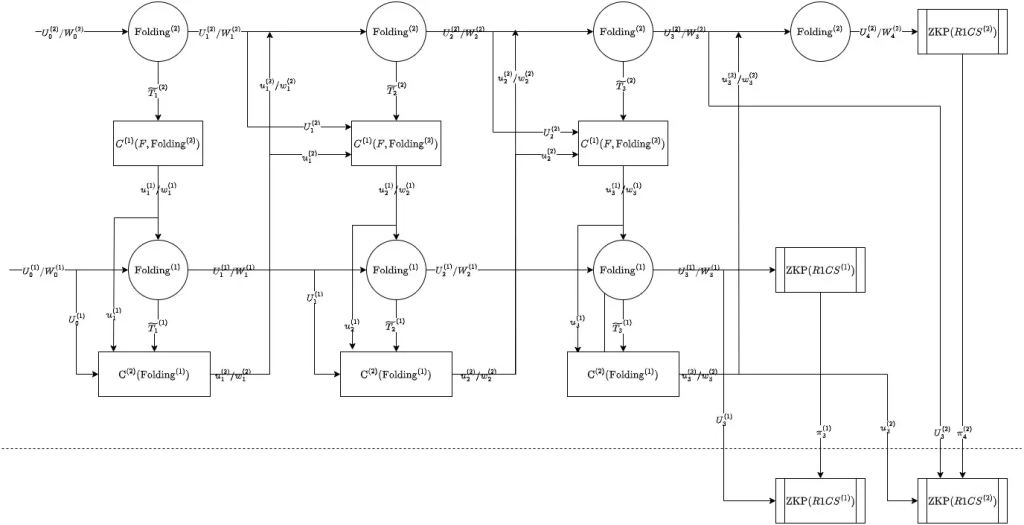
you might notice, we can actually from the second attempt, already write the folding process prover to \(F\), then we only have one accumulator, why not? this is because the \(F\) and prover are not working in the same field, one is the scaler field of an elliptic curve and one is the base field, so we need to use cycle of curves.