Using the following example to go through GKR protocol
this blogs follows the example in Spartan 预备知识:GKR with ZK Argument
zero knowledge version of GKR, Hyrax approach.
Parameters
Recall the parameters to capture the geometry of the circuit.
| \(N\) | number of identical copies of a base circuit \(C_0\) |
| \(G\) | number of gate within one layer of the base circuit \(C_0\) |
| \(b_G\) | \(2^{b_G}=G\) |
| \(b_N\) | \(2^{b_N}=N\) |
| \(q’\in \{0,1\}^{b_N}\) | The index of one of the \(N\) identical copies of the base circuit \(C_0\) within \(C\) |
| \(q\in \{0,1\}^{b_G}\) | the gate index within the base circuit |
| \(i\in [d]=\{0,1,…,D\}\) | the index of the layer within the base circuit |
| \(V(q’,q)\) | output value of gate \(q’,q\) at layer \(i\) |
| \(P_{q’,q,i}(h’,h_L,h_R)\) | function that captures the transaction from one layer to the next. Use this function to go through all the gates in layer \(i\) |
| \(h’\in \{0,1\}^{b_N}\) | The same definition of \(q’\), \(q’\) used as reference, \(h’\) goes through all the gates in the layer |
| \(h_R,h_L \in \{0,1\}^{b_G}\) | two gate indexs within the base circuit, the same as \(q\) but in layer \(i+1\) |
| \(add_i(q,h_L,h_R)\) | \(iff\) gate \(q\) at layer \(i\) takes both \(h_L\) and \(h_R\) as inputs from layer \(i+1\) and is an addition gate. (addition selector) |
| \(mul_i(q,h_L,h_R)=1\) | \(iff\) gate \(q\) at layer \(i\) takes both \(h_L\) and \(h_R\) as inputs from layer \(i+1\) and is a multiplication gate. (multiplication selector) |
| \(eq(h’,q’)\) | returns \(h’==q’\).limits only the gate that has index \(q’\) and on layer \(i-1\) (limited by \(V_{i+1}\)) can be counted. Recall \(q’\) is the index of one of \(N\) identical base circuit \(C_0\) with \(C\). |
Round 1 GKR layer 0
Prover sends the output (layer 0) of the circuit to the verifier, Verifier compute the multi-linear extension of the layer 0 polynomial. (Computation is in \(\mathbb{F}_5\))
\(i=0, N=2, b_N=1, G=2, b_G=1\)
verifier gets \(V_0=(0,2,3,1)\)
| \(q’\) | \(q\) | \(V_0(q’,q)\) |
| 0 | 0 | 0 |
| 0 | 1 | 2 |
| 1 | 0 | 3 |
| 1 | 1 | 1 |
by interpolation, verifier gets its multi-linear extension
\(s_0(x_1,x_2)=2x_2+3x_1-4x_1x_2\)
verifier choose challenge (2,4) and sends to prover, then we run into the sum-check protocol of layer 1. Prover needs to prove:
$$\widetilde{V_0}(q’,q)=\sum\limits_{h’\in \{0,1\}^{b_N}}\sum\limits_{h_L\in \{0,1\}^{b_G}}\sum\limits_{h_R\in \{0,1\}^{b_G}}P_{q’,q,1}(h’,h_L,h_R)$$
$$=\sum\limits_{h’\in \{0,1\}^{b_N}}\sum\limits_{h_L\in \{0,1\}^{b_G}}\sum\limits_{h_R\in \{0,1\}^{b_G}}\widetilde{eq_1}(q’,h’)\cdot [\widetilde{mul_1}(q,h_L,h_R)(\widetilde{V_1}(h’,h_L)\times \widetilde{V_1}(h’,h_R) )$$
$$+\widetilde{add_1}(q,h_L,h_R)(\widetilde{V_1}(h’,h_L)+ \widetilde{V_1}(h’,h_R) )]$$
$$\stackrel{?}{=}s_0(2,4)=2$$
Now the prover needs to compute the multilinear extension of polynomial \(P_{q’,q,1}(h’,h_L,h_R)\)
Let’s decompose it to 5 items and compute each of them separately:
| parameters | clarification |
| \(q’\) | \(q’=2\) as it is the challenger chosen by verifier |
| \(h’\) | \(h’\) is to go through all the copies of the base circuit in layer 1, \(h’\in \{0,1\}\) in this case |
How to compute the low degree extension of these functions? The answer is list all their values, and do “interpolation”, as shown below.
item 1 \(\widetilde{eq_1}(q’,h’)\)
| \(\widetilde{eq_1}(q’,h’)\) | q’ | h’ |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
as the table shows, \(\widetilde{eq_1}(x,y)\)=xy+(1-x)(1-y)=1-x-y+2xy
for \(q’=2\) , \(\widetilde{eq_1}(2,y_1)=3y_1-1\)
item 2 \(\widetilde{mul_1}(q,h_L,h_R)\)
as in a single base circuit \(C_0\), there are 4 wires (gates), we need two bits to represent \(h_L, h_R\)
| \(\widetilde{mul_1}(q,h_L,h_R)\) | \(q\) | \(h_L\) | \(h_R\) |
| 0 | 0 | 00 | 00 |
| … (all 0, as q=0, the first gate is addition gate) | … | 00 | … |
| 0 | 1 | 00 | 00 |
| …(all 0, as \(h_L=00/01, \) not the input wire) | … | 00,01 | … |
| … | 1 | … | … |
| 1 | 1 | 10 | 11 |
\(\widetilde{mul_1}(q,h_L,h_R)=\widetilde{mul_1}(y_1,(y_2,y_3),(y_4,y_5))=y_1y_2(1-y_3)y_4y_5\)
\(\widetilde{mul_1}(4,h_L,h_R)=4y_2(1-y_3)y_4y_5\)
item 3 \(\widetilde{add_1}(q,h_L,h_R)\)
(skip the LDE part)
\(\widetilde{add_1}(q,h_L,h_R)=-3(1-y_2)(1-y_3)(1-y_4)y_5\)
item 4 \(\widetilde{V_1}(h’,h_L)\)
| \(\widetilde{V_1}(y_1,(y_2,y_3))\) | \(y_1y_2y_3\) |
| 1 | 000 |
| 4 | 001 |
| 2 | 010 |
| 1 | 011 |
| 4 | 100 |
| 4 | 101 |
| 1 | 110 |
| 1 | 111 |
\(\widetilde{V_1}(h’,h_L)=(1-y_1)(1-y_2)(1-y_3)+4(1-y_1)(1-y_2)y_3+2(1-y_1)y_2(1-y_3)\)
\(+(1-y_1)y_2y_3+4y_1(1-y_2)(1-y_3)+4y_1(1-y_2)y_3+y_1y_2(1-y_3)+y_1y_2y_3\)
item 5 \(\widetilde{V_1}(h’,h_R)\)
\(\widetilde{V_1}(h’,h_R)=(1-y_1)(1-y_4)(1-y_5)+4(1-y_1)(1-y_4)y_5+2(1-y_1)y_4(1-y_5)\)
\(+(1-y_1)y_4y_5+4y_1(1-y_4)(1-y_5)+4y_1(1-y_4)y_5+y_1y_4(1-y_5)+y_1y_4y_5\)
notes: \(h_L\) and \(h_R\) need to be separated, therefore even through they are the same function, but we need to use different variables to present them (y_2, y_3,y_4,y_5)
Combine all the items and start sum-check protocol
How sumcheck protocol is embedded into GKR:
The gates \(\widetilde{add_1}(q,h_L,h_R)\) and \(\widetilde{mul_1}(q,h_L,h_R)\) already limits that only \(y_1y_2y_3y_4y_5=(y_1,0,0,0,1)\) and \(y_1y_2y_3y_4y_5=(y_1,1,0,1,1)\) needs to be considered, other values are 0.
The next step is to start sumcheck protocol in for verification of value \(V_0(2,4)\), but let’s have a look of the summation here
$$\widetilde{V_0}(q’,q)=\sum\limits_{h’\in \{0,1\}^{b_N}}\sum\limits_{h_L\in \{0,1\}^{b_G}}\sum\limits_{h_R\in \{0,1\}^{b_G}}P_{q’,q,1}(h’,h_L,h_R)$$
$$=\sum\limits_{h’\in \{0,1\}^{b_N}}\sum\limits_{h_L\in \{0,1\}^{b_G}}\sum\limits_{h_R\in \{0,1\}^{b_G}}\widetilde{eq_1}(q’,h’)\cdot [\widetilde{mul_1}(q,h_L,h_R)(\widetilde{V_1}(h’,h_L)\times \widetilde{V_1}(h’,h_R) )$$
$$+\widetilde{add_1}(q,h_L,h_R)(\widetilde{V_1}(h’,h_L)+ \widetilde{V_1}(h’,h_R) )]$$
in the equation, there are some low degree multi-linear extensions can be computed by verifier, namely
- item 1 \(\widetilde{eq_1}(q’,h’)\)
- item 2 \(\widetilde{mul_1}(q,h_L,h_R)\)
- item 3 \(\widetilde{add_1}(q,h_L,h_R)\)
But the following values are unknown to the verifier, as one needs to know the values of the gate
- item 4 \(\widetilde{V_1}(h’,h_L)\)
- item 5 \(\widetilde{V_1}(h’,h_R)\)
remember in the final step of the sumcheck protocol, verifier needs to check if the last polynomial given by the prover will agree with the same value as the low degree multilinear extension of the sumcheck polynomial with all the challenges as input. But if the verifier doesn’t know the multilinear extension at the beginning, how can he check that?
This is how sumcheck protocol is embedded into the GKR protocol, the unknown values will be the sumcheck values of next layer, and moves down until the input layer, where there are public inputs, and commitments for the private inputs from the prover before hand.
Sumcheck protocol on layer 0
Prover’s claim $$\widetilde{V_0}(2,4)=2$$
\(\sum\limits_{y_1\in \{0,1\}}\sum\limits_{y_2\in \{0,1\}}\sum\limits_{y_3\in \{0,1\}}\sum\limits_{y_4\in \{0,1\}}\sum\limits_{y_5\in \{0,1\}}…\) (product of the above 5 items)
Sumcheck round 1
set \(y_1\) is the only variable
\(s_1 (y_1)=2+2y_1+y_1^2=c_{0,1}+c_{1,1}y_1+c_{2,1}y_1^2\)
In sumcheck protocol, the prover is supposed to send \(s_1\) to the verifier, but to make it zero knowledge, prover can just send the commitment of the coefficients, verifier verifies by using the homeomorphic property. Namely, prover send:
$$\delta c_{0,1} = \text{commit}(c_{0,1}) = \text{commit}(2)$$
$$\delta c_{1,1} = \text{commit}(c_{1,1}) = \text{commit}(2)$$
$$\delta c_{2,1} = \text{commit}(c_{2,1}) = \text{commit}(1)$$
$$\delta c_{3,1} = \text{commit}(c_{3,1}) = \text{commit}(0)$$
Verifier verifies:
$$s_1(0) + s_1(1)\stackrel{?}{=}s_0(2,4)=\text{commit}(2)$$
via the homeomorphic property of the commitment, verfier actually checks
$$2\delta c_{0,1}+\delta c_{1,1} +\delta c_{2,1}+\delta c_{3,1}\stackrel{?}{=}\text{commit}(2)$$
Verifier chooses challenge \(y_1=3\), and in the next round, prover needs to prove
$$s_1(3)=2 \mod 5$$
Sumcheck round 2
Based on \(y_1=3\), in this round, prover computes
$$s_2(y_2)=8\cdot (-3)(1-y_2)(-11y_2+14)+8\cdot 4y_2\cdot(10-11y_2)$$
$$=4+4y_2^2$$
Prover sends the commitments for the coefficients to the verifier (I skip the details here), and verifier check if
$$s_2(0)+s_2(1)=s_1(3)$$
…. skip the detailed sumcheck procedures
Last step of Sumcheck protocol
assume the challenges are
\((3, (4,2), (4,1)) = (y_1, (y_2, y_3), (y_4, y_5)) = (r’, r_L, r_R)\)
Prover commits to
$$X=\text{commit}(V_1(r’, r_L)) = \text{commit}(V_1(3, (4, 2))) = \text{commit}(3)$$
$$Y=\text{commit}(V_1(r’, r_R)) = \text{commit}(V_1(3, (4, 1))) = \text{commit}(2)$$
$$Z=\text{commit}(V_1(r’, r_L) \cdot V_1(r’, r_R)) = \text{commit}(3 \cdot 2) = \text{commit}(1)$$
Having these three commitments, verifier can do the last check for the sumcheck protocol
$$\widetilde{eq_1}(2,3)\cdot [\widetilde{mul_1}(4,(4,2),(4,1))(\text{commit}(\widetilde{V_1}(3,(4,2))\times \widetilde{V_1}(3,(4,1))) )$$
$$+\widetilde{add_1}(4,(4,2),(4,1))(\widetilde{V_1}(3,(4,2))+ \widetilde{V_1}(3,(4,1)) )]$$
$$=8\cdot[-64\cdot \text{commit}(1)+27\cdot(\text{commit}(3)+\text{commit}(2) )]= \text{commit}(3)$$
Sumcheck protocol on layer 1
Prover claims commitments for \(\widetilde{V_1}(3, (4, 2))\) and \(\widetilde{V_1}(3, (4, 1))\) in the last round of layer 0 sumcheck protocol, these two values then become the values that prover wants to prove in the sumcheck protocol of layer 1. However, if every round of sumcheck protocol there will be one more value need to be proved, then the proving work will grow exponentially. To avoid this, a fold factor is introduced, folding the two claims to be one.
$$f_H(t)=\widetilde{V_1}(r’, (1-t)\cdot r_L+t\cdot r_R)$$
and
$$f_H(0)=\widetilde{V_1}(r’, r_L)=\widetilde{V_1}(3, (4, 2))=3$$
$$f_H(1)=\widetilde{V_1}(r’, r_R)=\widetilde{V_1}(3, (4, 1))=2$$
$$f_H(t)=3+4t$$
Having \(f_H(t)\), in the previous round of sumcheck protocol, in the last check, prover can send the commitment of \(f_H\), namely, the commitment for its coefficients, to the verifier,
$$\delta_{f_0} = \text{commit}(3)$$
$$\delta_{f_1} = \text{commit}(4)$$
$$\delta_{f_2} = \text{commit}(0)$$
verifier can compute \(X,Y\) and verifier the last check.
$$\text{commit}(f_H(0))=\delta_{f_0}$$
$$\text{commit}(f_H(1))=\delta_{f_0}+\delta_{f_1}$$
and the sumcheck on layer 1 becomes the verification for
$$\widetilde{V_1}(3, (4, 2(1-t)+t))=\widetilde{V_1}(3, (4, 2-t))=3+4t$$
skip details of this step.
Final sumcheck
The sumcheck of layer 1 will end up with two commitment need to be verified in layer 2. Assuming they are
$$\widetilde{V_2}(2, (3, 2))=0$$
$$\widetilde{V_2}(2, (3, 3))=1$$
prover gets:
$$f_H(t)=t$$
assuming folding factor is 2, the check becomes
$$\widetilde{V_2}(2, (3, 4))\stackrel{?}{=}f_H(2)=2$$
prover sends the commitments for \(f_H\) and verifier computs
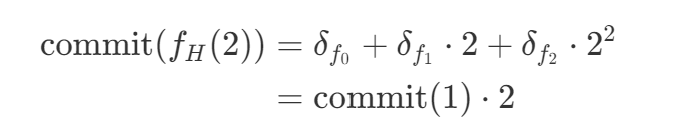
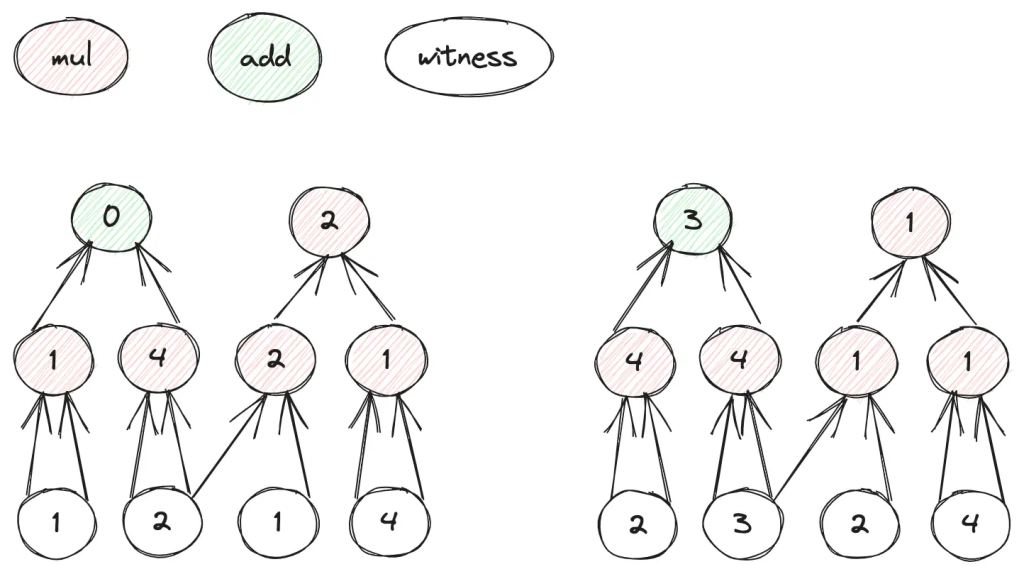
come back to the circuit
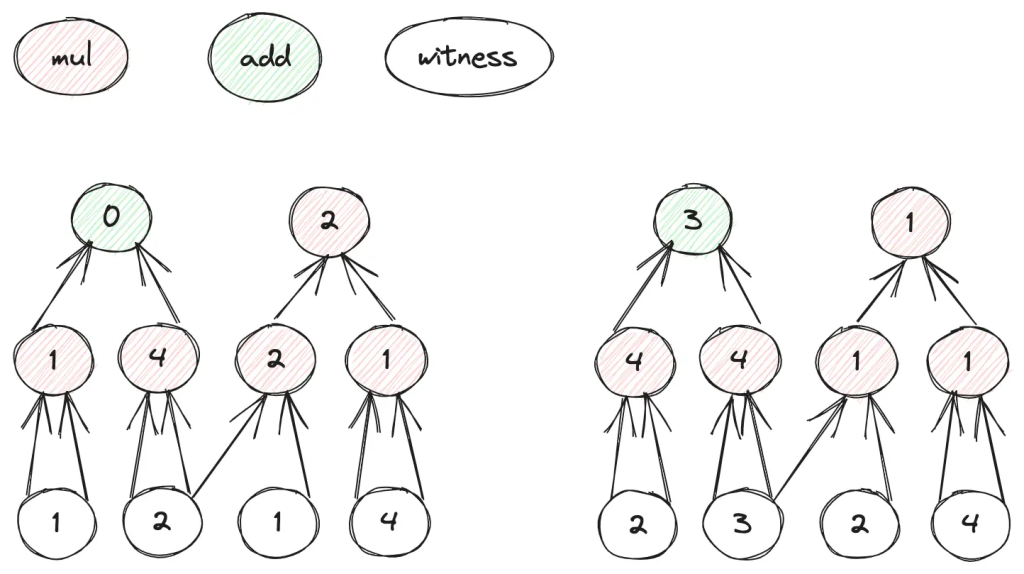
in layer 2, there are public inputs and private inputs
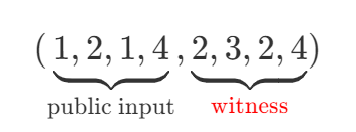
we can split \(\widetilde{V_2}\) to be two parts
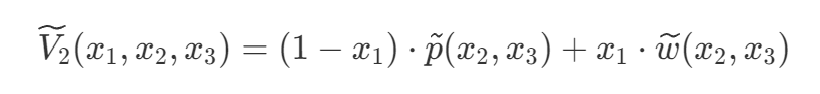
for the public part \(\tilde{p}(x_2,x_3)\), verifier can computes MLE by itself. for witness part, verifier at the beginning receives the commitments for each witness, the MLE for \(\tilde{w}(x_2,x_3)\) can be computed as well.
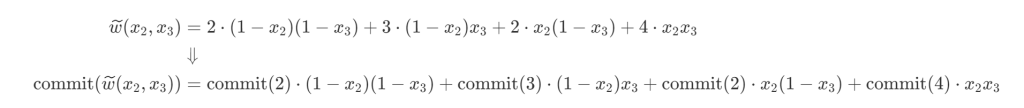
put everything together

My unsolved questions
- When these commitments are generated
$$X=\text{commit}(\widetilde{V_1}(r’, r_L)) = \text{commit}(\widetilde{V_1}(3, (4, 2))) = \text{commit}(3)$$
$$Y=\text{commit}(\widetilde{V_1}(r’, r_R)) = \text{commit}(\widetilde{V_1}(3, (4, 1))) = \text{commit}(2)$$
$$Z=\text{commit}(\widetilde{V_1}(r’, r_L) \cdot \widetilde{V_1}(r’, r_R)) = \text{commit}(3 \cdot 2) = \text{commit}(1)$$
how to verify \(Z\) is the commitment for the product of the openings of \(X\) and \(Y\), and if this verification is necessary?
2. the verifier chooses many challenges, a bit messy. it is not very clear the order of each challenge is chosen and the generation of each commitment.