Author: shuangcrypto.com

Logup-GKR batching concept

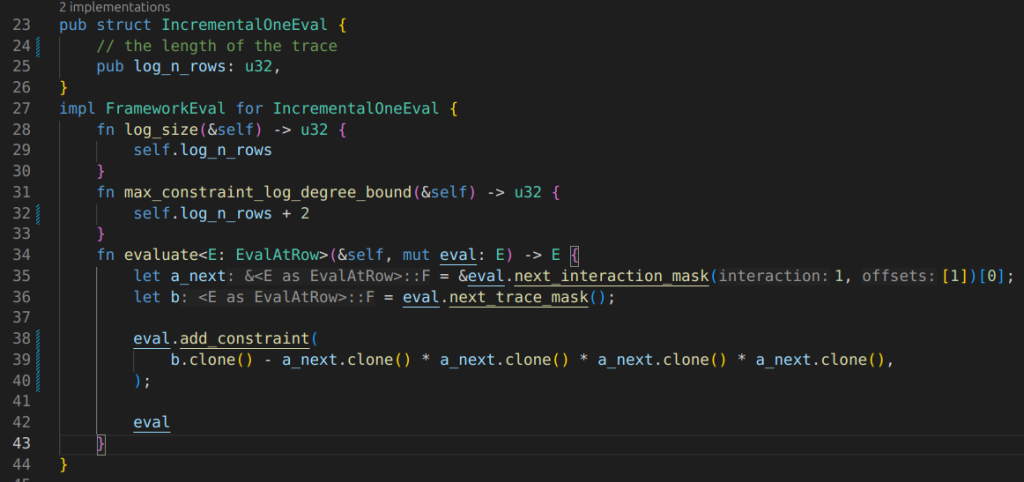
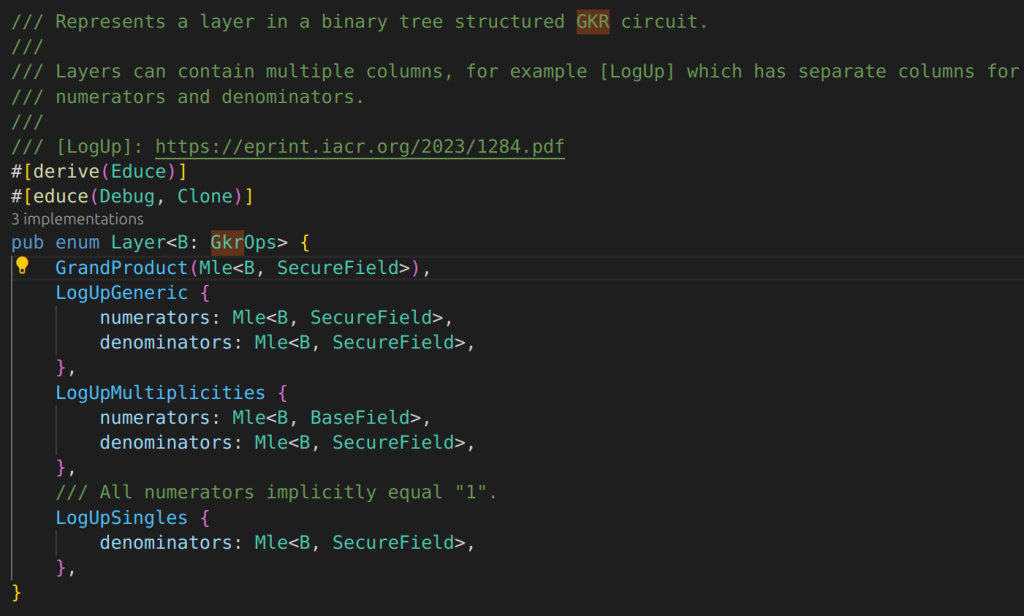
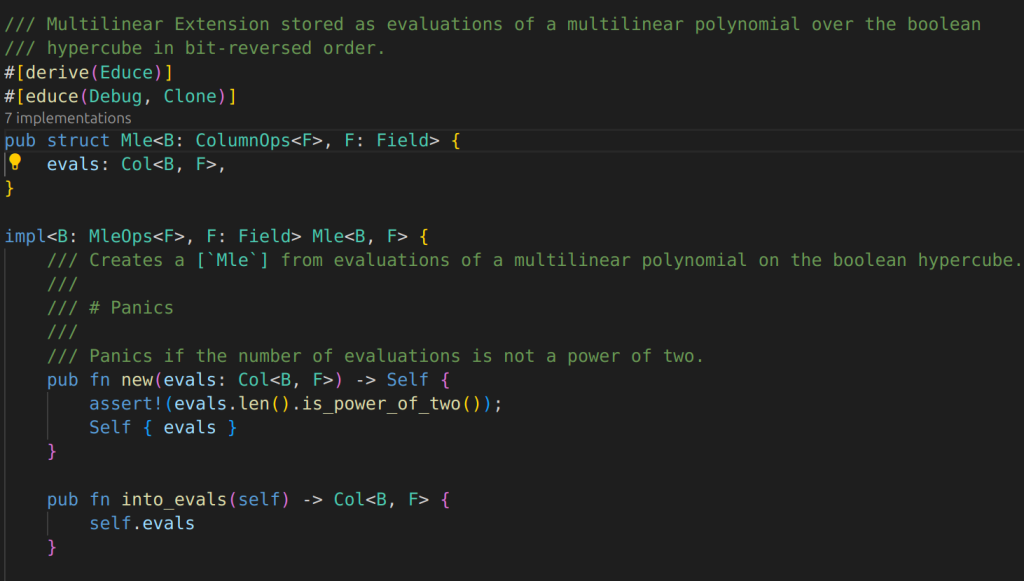
IOP: prove evaluation of a multi-linear extension polynomial

a cyclic group in base Field \( \mathbb{H} \) (STARK trace domain)

base Field \(\mathcal{F}\)

4th degree extension of base Field, Secure Field \(\mathcal{SF}\)

\(a(w)\) is a univariate polynomial of degree \(2^d\) (STARK trace), \(w\in \mathbb{H}\)

\(f(b_0,b_1,…,b_d)\) is a multi-variate function (STARK …

Logup GKR in an example

traces:

\(a: [a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7]\)

\(b: [b_0,b_1,b_2,b_3,b_4,b_5,b_6,b_7]\)

goal:

prove logup relation:

\(\sum\limits_{i=0}^{i=7}\frac{1}{a_i+\alpha}=\sum\limits_{i=0}^{i=7}\frac{1}{b_i+\alpha}\)

what are available:
  • commitments to the traces via FIR:

\(\text{commit}[a(x)]\)

\(\text{commit}[b(x)]\)

note: \(a(x),b(x)\) denote the polynomials’ evaluation in trace domain, \(x\) comes from cyclic group.

  • GKR circuit: give a proof for the accumulation of fractions, reduced the problem to proving
…

logup GKR stwo implementation steps

Include challenge in input MLE

question 1: the challenge in logup denominators are really necessary to be in MLE?

yes, this challenge is irrelevant to the GKR protocol (don’t mess it with the challenges in sum-check and challenges for later random linear combination of MLE evaluations), \(\frac{1}{\alpha +x}\) \(\alpha\) guarantees …

Stwo logup-GKR : build test example

step 1: get the most important 2 ingredients:

when create a component like this:

there are two important thing:

  • FrameworkComponent
  • eval that implement FrameworkEval

we can see the example actually use two types of Component, one is from FrameworkComponent (MleCoeffColumnComponent), one is from MleEvalProverComponent, which is defined specifically for MLE …

Logup GKR – 3: Air constraint for STARK

Committed Traces

The traces that will be interpreted as multilinear polynomial evaluations from STARK:

talking about a single lookup relation, for multiple lookup, it means the

Extra traces that dedicated for Logup-GKR and need to be built additionally

Circuit Example:

using a simple example to describe the GKR circuit

bus …

Logup GKR 2

following previous post

Input Layer Encoding (witness encoding)

trace columns are interpreted as functions, the inputs of the function are bits, enough number of bits that can present \(n\) number of witness in this column.

for trace \(i\), with \(n\) number of rows (trace degree, trace length)

\(f_i(b_0,b_1,b_2,…,b_n)=a_{b_n,…,b_2,b_1,b_0} \)

at …

Logup GKR

following this post

Witness encoding:

trace columns are interpreted as functions, the inputs of the function are bits, enough number of bits that can present \(n\) number of witness in this column.

for trace \(i\), with \(n\) number of rows (trace degree, trace length)

\(f_i(b_0,b_1,b_2,…,b_n)=a_{b_n,…,b_2,b_1,b_0} \)

the multi-linear polynomial for …

Commonly used tricks in Multilinear polynomials

Equation function

Turn a function in binary field to its multilinear extension.

let \(\mathcal{G}\) be a function in binary field, its multi-linear extension can be presented as:

$$\mathcal{G}(r_1,…,r_m)=\sum\limits_{x\in\{0,1\}^m}\mathcal{G}(x)\prod\limits^{m}_{i=1}\underbrace{(r_i\cdot x_i + (1-r_i)(1-x_i))}_{x_i=0 \rightarrow 1-r_i, x=1 \rightarrow r_i }$$

emphasize:

\(r_i \in \mathbb{F}\)

\(x \in \{0,1\}^m\)

\(x_i \) is 0 or 1…

High degree constraint in Plonky3 and Stwo

How to define high degree constraint in Plonky3 and Stwo as a user

Plonky3:

A user must verify the following equation when determining the degree of the constraint (further explanation is provided in the next section):

let \(d\) be the degree of the constraint:

\(d-1\leq 2^{\text{log_blow_up_factor}}\)

If this condition is …