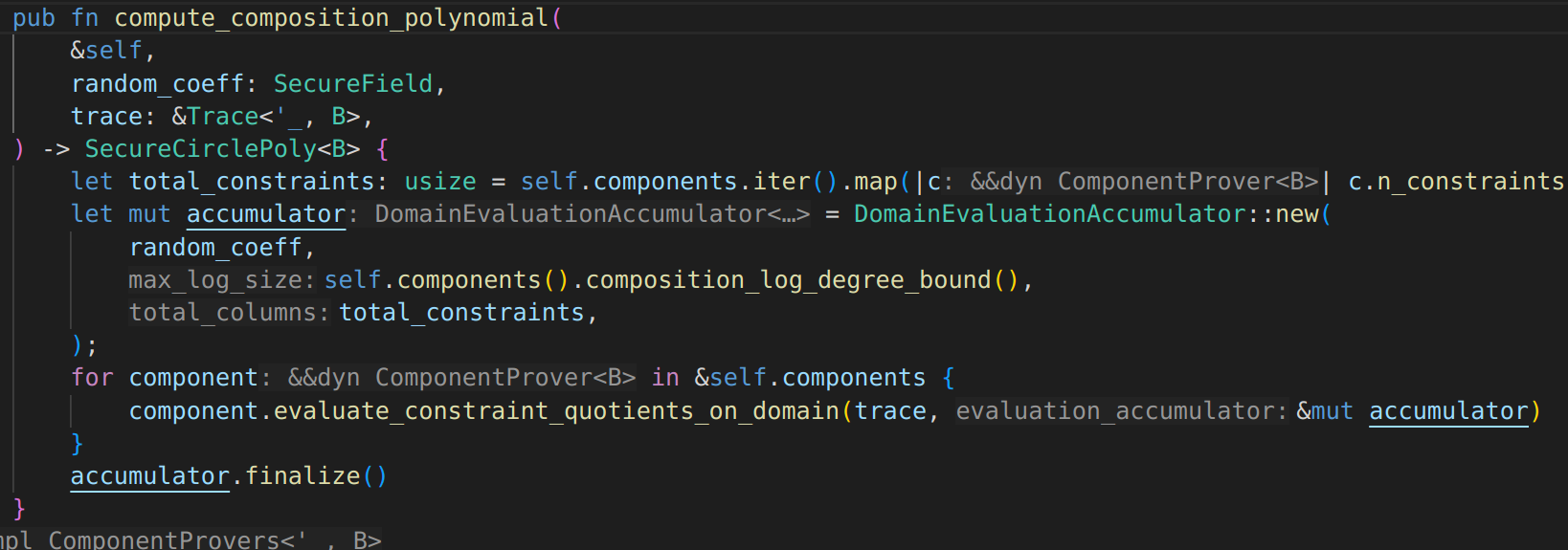
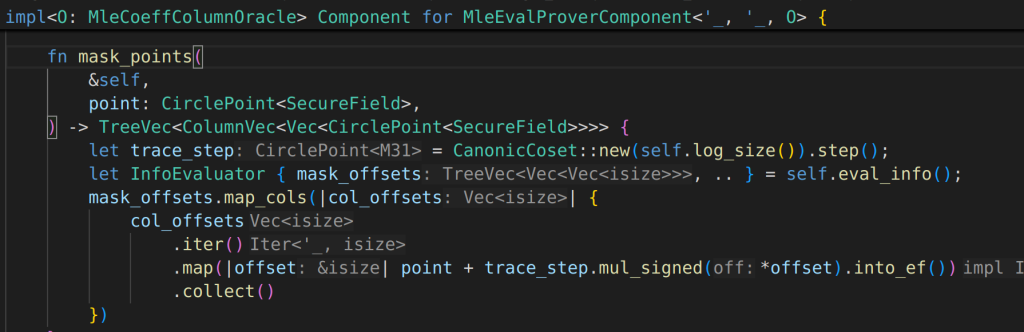
I am using a simplified circuit for case demonstration purpose:
The bus statement to be proved is:
\([x_0,x_1]\) in [0] with \(bus_{id}\)=a,
this case has only one valid witness [0,0], with multiplicity to be 2
Original protocol:
The above statement essentially proves:
\(\frac{1}{\alpha -x_0}+\frac{1}{\alpha -x_1}=\frac{2}{\alpha}\)
where \(\alpha\) is a random …