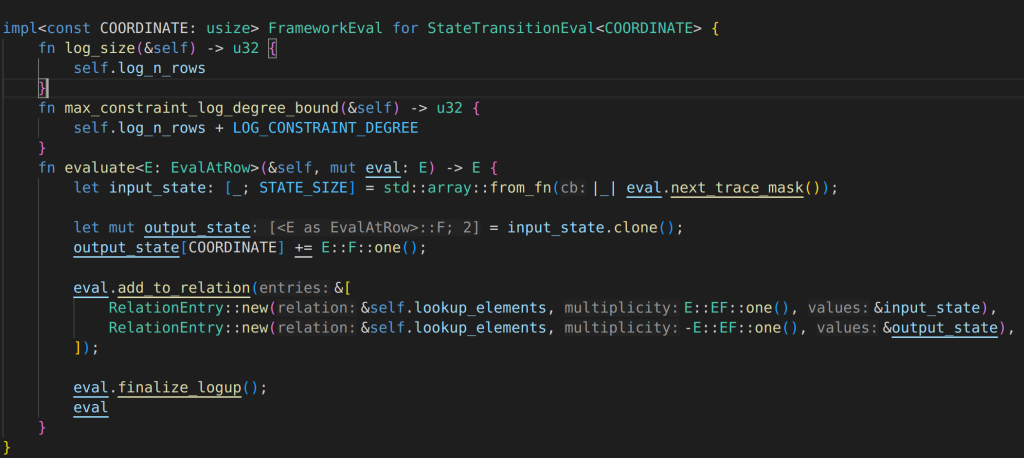
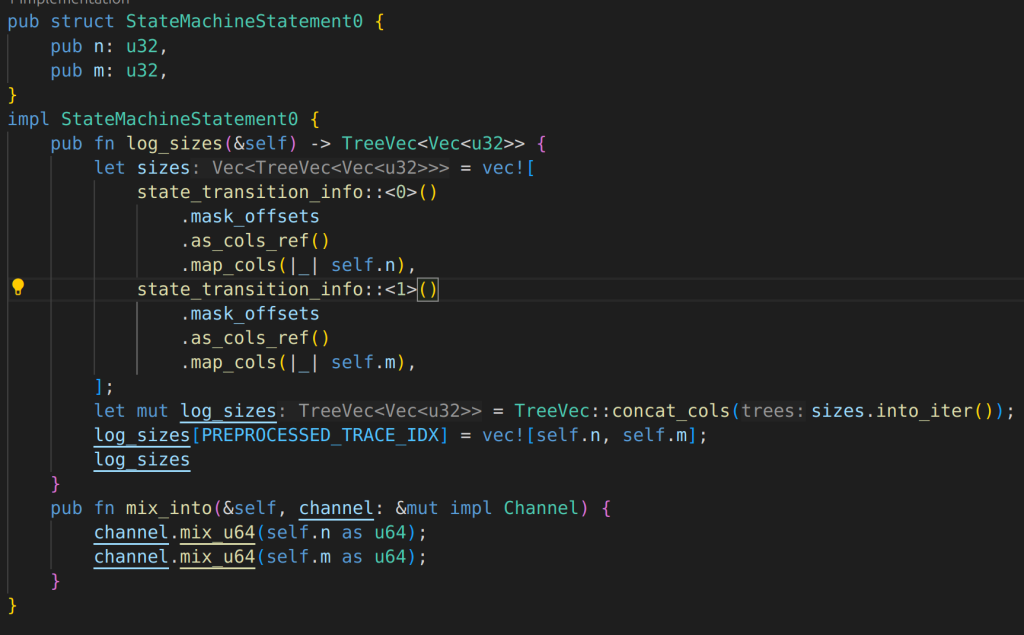
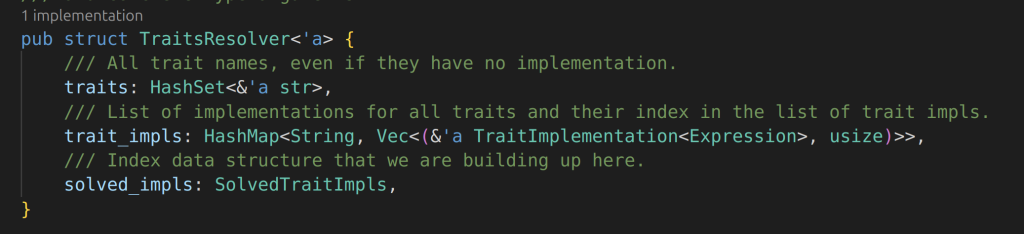
Start with the proof of stwo:

commitmentSchemeProof
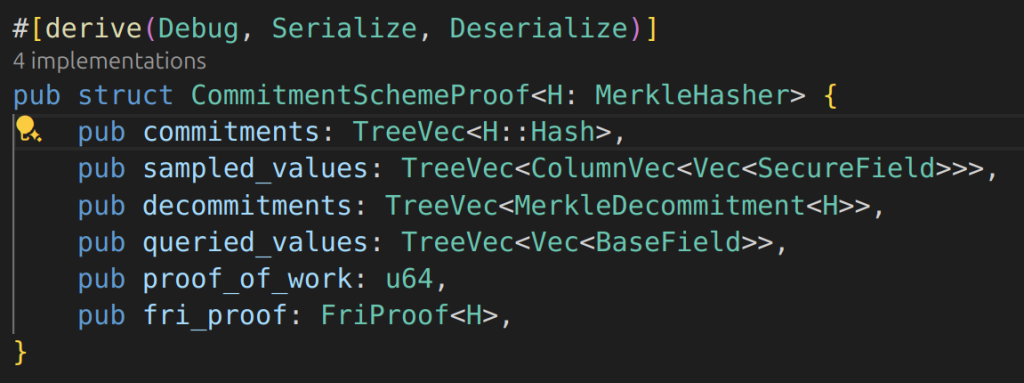
proof.commitments
contains the proof info, the interesting part is the commitments, in the verification function, there will be commitments[0], commitments[1],commitments[2] represent the commitment of pre-process trace, witness trace and lookup trace commitments. namely, they only have three root commitments, every root commitment should …