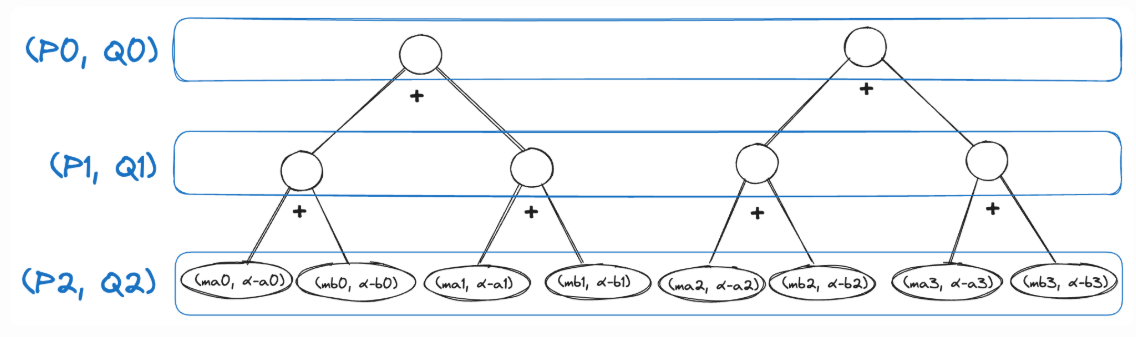
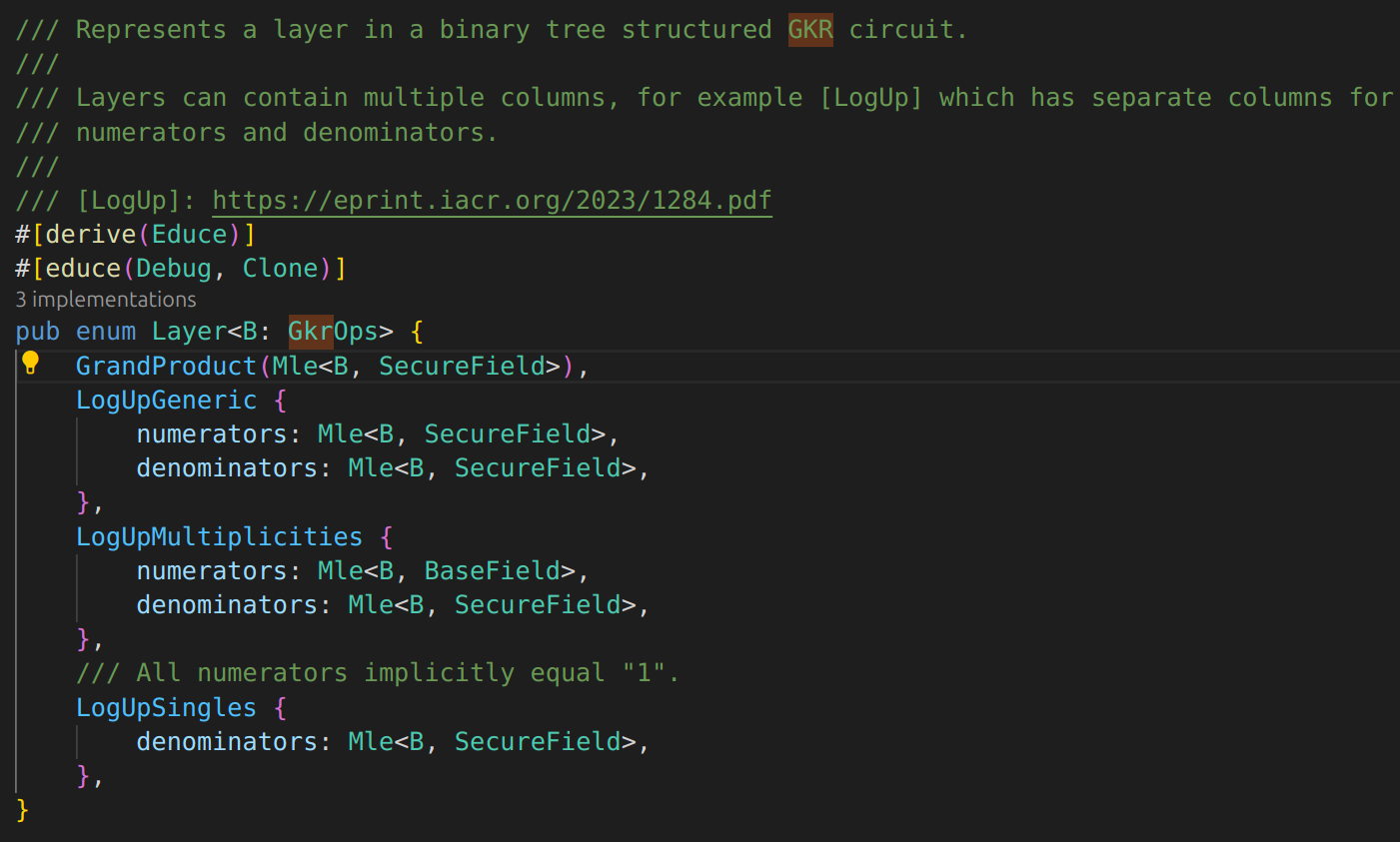
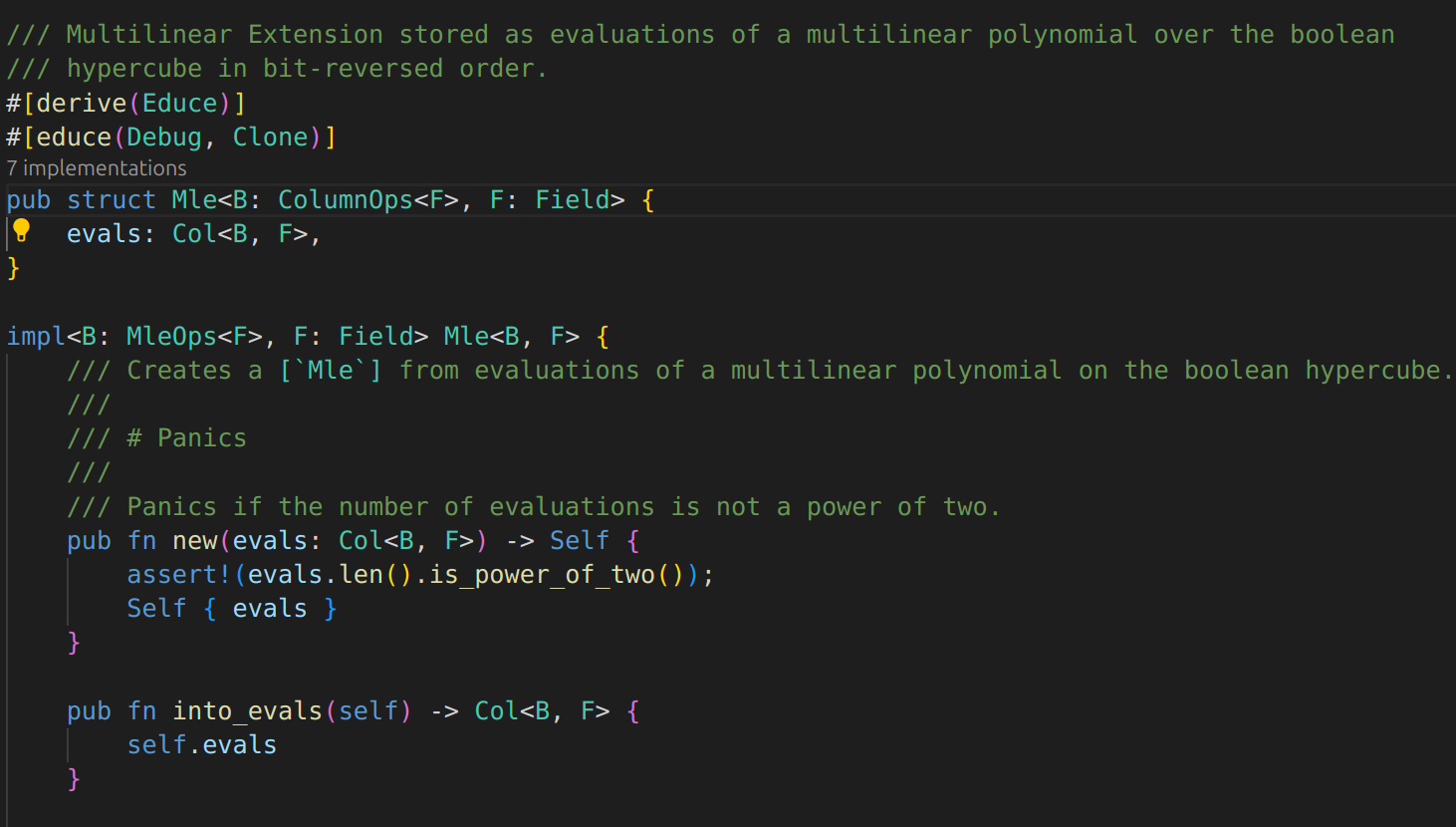
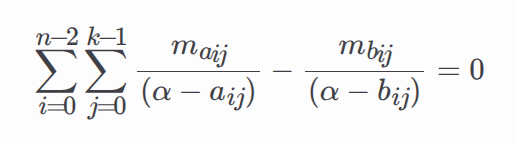Canonical coset:
odd coset setup
CirclePointIndex is just a wrapper of usize, which represent actually the order of the coset generator.

when creating a new coset, we need a generator and shiftoffset, the shiftoffset mostly be the generator of the subgroup of one log size bigger

so here, CirclePointIndex::subgroup_gen is …