Category: Zero Knowledge Proof

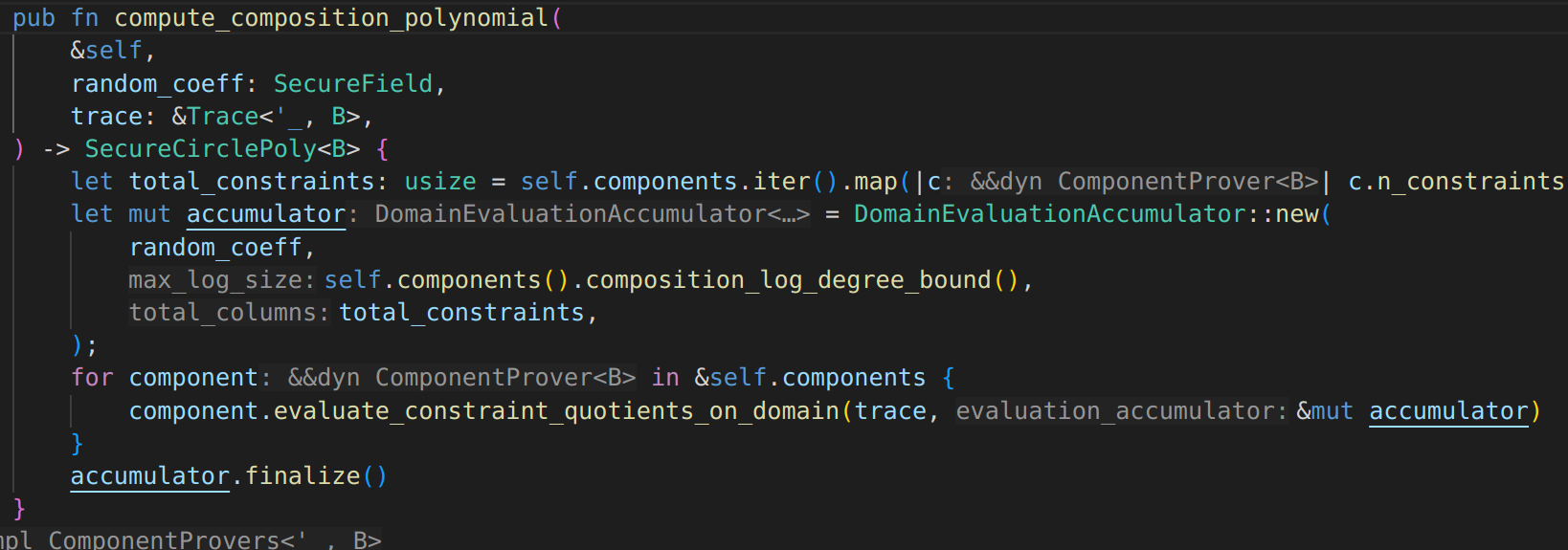
There are different ways to describe the GKR algorithm

from Libra paper:

\(\tilde{V}_i(g) = \sum\limits_{x,y \in \{0,1\}^{s_{i+1}}} f_i(x,y)\)

\(= \sum\limits_{x,y \in \{0,1\}^{s_{i+1}}} \left( \widetilde{add}_{i+1}(g,x,y)(\tilde{V}_{i+1}(x) + \tilde{V}_{i+1}(y))\right.\)

\(\left. + \tilde{mult}_{i+1}(g,x,y)(\tilde{V}_{i+1}(x)\tilde{V}_{i+1}(y)) \right)\)

from hyrax paper:

$$\widetilde{V_0}(q’,q)=\sum\limits_{h’\in \{0,1\}^{b_N}}\sum\limits_{h_L\in \{0,1\}^{b_G}}\sum\limits_{h_R\in \{0,1\}^{b_G}}P_{q’,q,1}(h’,h_L,h_R)$$

$$=\sum\limits_{h’\in \{0,1\}^{b_N}}\sum\limits_{h_L\in \{0,1\}^{b_G}}\sum\limits_{h_R\in \{0,1\}^{b_G}}\widetilde{eq_1}(q’,h’)$$

$$\cdot [\widetilde{mul_1}(q,h_L,h_R)(\widetilde{V_1}(h’,h_L)\times \widetilde{V_1}(h’,h_R) )$$

$$+\widetilde{add_1}(q,h_L,h_R)(\widetilde{V_1}(h’,h_L)+ \widetilde{V_1}(h’,h_R) )]$$…

performance:

Prover is \(\mathcal{O}(C)\)

Verifier is \(\mathcal{O}(d\log C)\) for d-depth log-space uniform circuit.

note: in sumcheck/GKR context, the size of the circuit usually is described as \(2^l\), namely, the inputs of the circuit is \(2^l\), for a linear prover in this setting, has complexity \(\mathcal{O}(2^l)\), a logarithmic verifier has \(\mathcal{O}(l)\) …

R1CS encoding

R1CS instance \(x=(\mathbb{F},A,B,C,io,m,n)\)

let \(Z=(io,1,w)\), then we have for example

\(\underbrace{\begin{bmatrix}0&1&1&0\\0&0&1&0\\…&…&…&..\\…&…&…&..\end{bmatrix}}_{A}\begin{pmatrix}w_1\\1\\w_2\\w_3\end{pmatrix}\circ \underbrace{\begin{bmatrix}0&1&0&0\\0&0&1&0\\…&…&…&..\\…&…&…&..\end{bmatrix}}_{B}\begin{pmatrix}w_1\\1\\w_2\\w_3\end{pmatrix}\)

\(=\underbrace{\begin{bmatrix}1&0&0&0\\0&0&0&1\\…&…&…&..\\…&…&…&..\end{bmatrix}}_{C}\begin{pmatrix}w_1\\1\\w_2\\w_3\end{pmatrix}\)

This express the constraints:

$$(1+w_2) \cdot 1=w_1$$

$$w_2 \cdot w_2=w_3$$

In order to use the sum-check protocol, we need to encode R1CS in a different way, as sum-check is about …

A Folding Scheme for Committed Relaxed R1CS

…

Take example circuit in figure 1, following the Arithmetization described in post, a step by step description of GKR arithmetication of a concrete example.

Notations representing index of gates

\(q’\in \{0,1\}^{b_N}\): The index of one of the \(N\) identical copies of the base circuit \(C_0\) within \(C\).…

To understand the attack on Nova, I figure out I need to understand the role of the hash function and the validation check of hash function in Nova, from the first paper where the “cycle of curves” is not introduced, the circuit is illustrated as

to …

explain the multipoints opening of Halo 2, I don’t think Halo2 book explain this part clearly, and perhaps, neither my note.

the key, is the homomorphism of the commitment scheme. and combine the evaluation at different points, and combine the different polynomial evaluated at the same points. Later if I …

Stark can be described in 5 steps in a high level:

1. Computation program
2. generate an execution trace and a set of polynomial constraints, AIR (Algebraic Intermediate Representation) (no circuit)
3. Transfer the execution trace to be a polynomial, extend it to a larger domain
4. compute the composition polynomial, which is the

…